Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-23T19:32:01.206Z Has data issue: false hasContentIssue false
  • English
  • Français

On the circle criterionfor boundarycontrol systemsin factor form: Lyapunov stability and Lur'e equations

Published online by Cambridge University Press:  15 December 2005

Piotr Grabowski  and
Frank M. Callier
Piotr Grabowski
Affiliation:
Institute of Automatics, AGH University of Science and Technology, avenue A. Mickiewicz 30, B1, rm.314, 30-059 Cracow, Poland; [email protected]
Frank M. Callier
Affiliation:
University of Namur (FUNDP), Department of Mathematics, Rempart de la Vierge 8, 5000 Namur, Belgium; [email protected]
Get access

Abstract

A Lur'e feedback control system consisting of a linear, infinite-dimensional system of boundary control in factor form and a nonlinear static sector type controller is considered. A criterion of absolute strong asymptotic stability of the null equilibrium is obtained using a quadratic form Lyapunov functional. The construction of such a functional is reduced to solving a Lur'e system of equations. A sufficient strict circle criterion of solvability of the latter is found,which is based on results by Oostveen and Curtain [Automatica34 (1998) 953–967]. All theresults are illustrated in detail by an electrical transmission line example of thedistortionless loaded $\mathfrak{RLCG}$ 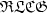-type. The paper uses extensively thephilosophy of reciprocal systems with bounded generating operators as recentlystudied and used by Curtain in (2003) [Syst. Control Lett.49 (2003) 81–89; SIAM J. Control Optim.42 (2003) 1671–1702].

Keywords

Infinite-dimensional control systemssemigroupsLyapunovfunctionalscircle criterion.
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 12 , Issue 1 , January 2006 , pp. 169 - 197
Copyright
© EDP Sciences, SMAI, 2006

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arendt, W. and Batty, C.J.K., Tauberian theorems and stability of one-parameter semigroups. Trans. Amer. Math. Soc. 306 (1988) 837–852. CrossRef
Balakrishnan, A.V., On a generalization of the Kalman-Yacubovic lemma. Appl. Math. Optim. 31 (1995) 177–187. CrossRef
Bucci, F., Frequency domain stability of nonlinear feedback systems with unbounded input operator. Dynam. Contin. Discrete Impuls. Syst. 7 (2000) 351–368.
Callier, F.M. and Winkin, J., LQ-optimal control of infinite-dimensional systems by spectral factorization. Automatica 28 (1992) 757–770. CrossRef
Curtain, R.F., Linear operator inequalities for strongly stable weakly regular linear systems. Math. Control Signals Syst. 14 (2001) 299–337. CrossRef
Curtain, R.F., Regular linear systems and their reciprocals: application to Riccati equations. Syst. Control Lett. 49 (2003) 81–89. CrossRef
Curtain, R.F., Riccati equations for stable well-posed linear systems: The generic case. SIAM J. Control Optim. 42 (2003) 1671–1702. CrossRef
R.F. Curtain and H. Zwart, An Introduction to Infinite-Dimensional Linear Systems Theory. Heidelberg, Springer (1995).
Curtain, R.F., Logemann, H. and Staffans, O., Stability results of Popov-type for infinite – dimensional systems with applications to integral control. Proc. London Math. Soc. 86 (2003) 779–816. CrossRef
H. Górecki, S. Fuksa, P. Grabowski and A.Korytowski, Analysis and Synthesis of Time-Delay Systems. Warsaw & Chichester: PWN and J. Wiley (1989).
Grabowski, P., On the spectral – Lyapunov approach to parametric optimization of DPS. IMA J. Math. Control Inform. 7 (1990) 317–338. CrossRef
Grabowski, P., The LQ controller problem: an example. IMA J. Math. Control Inform. 11 (1994) 355–368. CrossRef
Grabowski, P., On the circle criterion for boundary control systems in factor form. Opuscula Math. 23 (2003) 1–25.
P. Grabowski and F.M. Callier, Admissible observation operators. Duality of observation and control using factorizations. Dynamics Continuous, Discrete Impulsive Systems 6 (1999) 87–119.
P. Grabowski and F.M. Callier, On the circle criterion for boundary control systems in factor form: Lyapunov approach. Facultés Universitaires Notre-Dame de la Paix à Namur, Publications du Département de Mathématique, Research Report 07 (2000), FUNDP, Namur, Belgium.
Grabowski, P. and Callier, F.M., Boundary control systems in factor form: Transfer functions and input-output maps. Integral Equations Operator Theory 41 (2001) 1–37. CrossRef
Grabowski, P. and Callier, F.M., Circle criterion and boundary control systems in factor form: Input-output approach. Internat. J. Appl. Math. Comput. Sci. 11 (2001) 1387–1403.
P. Grabowski and F.M. Callier, On the circle criterion for boundary control systems in factor form: Lyapunov stability and Lur'e equations. Facultés Universitaires Notre-Dame de la Paix à Namur, Publications du Département de Mathématique, Research Report 05 (2002), FUNDP, Namur, Belgium.
U. Grenander and G. Szegö, Toeplitz Forms and Their Application, Berkeley: University of California Press (1958).
K. Hoffman, Banach Spaces of Analytic Functions. Englewood Cliffs: Prentice-Hall (1962).
Lasiecka, I. and Triggiani, R., Differential and Algebraic Riccati Equations with Application to Boundary/Point Control Problems: Continuous Theory and Approximation Theory. Lect. Notes Control Inform. Sci. 164 (1991) 1–160. CrossRef
I. Lasiecka and R. Triggiani, Control Theory for Partial Differential Equations: Continuous and Approximation Theories. Part I: Abstract Parabolic Systems, Cambridge: Cambridge University Press, Encyclopedia Math. Appl. 74 (2000).
I. Lasiecka and R. Triggiani, Control Theory for Partial Differential Equations: Continuous and Approximation Theories. Part II: Abstract Hyperbolic-Like Systems over a Finite Time Horizon, Cambridge: Cambridge University Press, Encyclopedia Math. Appl. 75 (2000).
Likhtarnikov, A.L. and Yacubovich, V.A., The frequency domain theorem for continuous one-parameter semigroups, IZVESTIJA ANSSSR. Seria matematicheskaya. 41 (1977) 895–911 (in Russian).
Logemann, H. and Curtain, R.F., Absolute stability results for well-posed infinite-dimensional systems with low-gain integral control. ESAIM: COCV 5 (2000) 395–424. CrossRef
Louis, J.-Cl. and D.Wexler, The Hilbert space regulator problem and operator Riccati equation under stabilizability. Annales de la Société Scientifique de Bruxelles 105 (1991) 137–165.
Lyubich, Yu. and Phong, Vû Quôc, Asymptotic stability of linear differential equations in Banach spaces. Studia Math. 88 (1988) 37–41.
Noldus, E., On the stability of systems having several equilibrium points. Appl. Sci. Res. 21 (1969) 218–233. CrossRef
Noldus, E., Galle, A. and Jasson, L., The computation of stability regions for systems with many singular points. Intern. J. Control 17 (1973) 641–652. CrossRef
Noldus, E., New direct Lyapunov-type method for studying synchronization problems. Automatica 13 (1977) 139–151. CrossRef
Nudel'man, A.A. and Schwartzman, P.A., On the existence of solution of some operator inequalities. Sibirsk. Mat. Zh. 16 (1975) 563–571 (in Russian).
Oostveen, J.C. and Curtain, R.F., Riccati equations for strongly stabilizable bounded linear systems. Automatica 34 (1998) 953–967. CrossRef
Pandolfi, L., Kalman-Popov-Yacubovich theorem: an overview and new results for hyperbolic control systems. Nonlinear Anal. Theor. Methods Appl. 30 (1997) 735–745. CrossRef
L. Pandolfi, Dissipativity and Lur'e problem for parabolic boundary control system, Research Report, Dipartamento di Matematica, Politecnico di Torino 1 (1997) 1–27; SIAM J. Control Optim. 36 (1998) 2061–2081.
Pandolfi, L., The Kalman-Yacubovich-Popov theorem for stabilizable hyperbolic boundary control systems. Integral Equations Operator Theory 34 (1999) 478–493. CrossRef
A. Pazy, Semigroups of Linear Operators and Applications to Partial Differential Equations. New York, Springer-Verlag (1983).
Salamon, D., Realization theory in Hilbert space. Math. Systems Theory 21 (1989) 147–164. CrossRef
Staffans, O.J., Quadratic optimal control of stable well-posed linear systems through spectral factorization. Math. Control Signals Systems 8 (1995) 167–197. CrossRef
Staffans, O.J. and Weiss, G., Transfer functions of regular linear systems, Part II: The system operator and the Lax-Phillips semigroup. Trans. Amer. Math. Soc. 354 (2002) 3229–3262. CrossRef
M. Vidyasagar, Nonlinear Systems Analysis. 2nd Edition, Englewood Cliffs NJ, Prentice-Hall (1993).
Weiss, G., Transfer functions of regular linear systems. Part I: Characterization of regularity. Trans. AMS 342 (1994) 827–854.
M. Weiss, Riccati Equations in Hilbert Spaces: A Popov function approach. Ph.D. Thesis, Rijksuniversiteit Groningen, The Netherlands (1994).
Weiss, M. and Weiss, G., Optimal control of stable weakly regular linear systems. Math. Control Signals Syst. 10 (1997) 287–330. CrossRef
R.M. Young, An Introduction to Nonharmonic Fourier Series. New York, Academic Press (1980).