Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Carlier, Guillaume
and
Tahraoui, Rabah
2010.
Hamilton-Jacobi-Bellman equations for the optimal control of a state equation with memory.
ESAIM: Control, Optimisation and Calculus of Variations,
Vol. 16,
Issue. 3,
p.
744.
Bonnans, Joseph Frédéric
and
Sánchez Fernández de la Vega, Constanza
2010.
Optimal Control of State Constrained Integral Equations.
Set-Valued and Variational Analysis,
Vol. 18,
Issue. 3-4,
p.
307.
Buttazzo, G.
Carlier, G.
and
Tahraoui, R.
2010.
On Some Systems Controlled by the Structure of Their Memory.
SIAM Journal on Control and Optimization,
Vol. 48,
Issue. 8,
p.
5241.
Federico, Salvatore
Goldys, Ben
and
Gozzi, Fausto
2011.
HJB Equations for the Optimal Control of Differential Equations with Delays and State Constraints, II: Verification and Optimal Feedbacks.
SIAM Journal on Control and Optimization,
Vol. 49,
Issue. 6,
p.
2378.
Skandari, Mohammad Hadi Noori
Erfanian, Hamid Reza
and
Kamyad, Ali Vahidian
2011.
A New Approach for a Class of Optimal Control Problems of Volterra Integral Equations.
Intelligent Control and Automation,
Vol. 02,
Issue. 02,
p.
121.
Cannarsa, P.
Frankowska, H.
and
Marchini, E. M.
2013.
Optimal control for evolution equations with memory.
Journal of Evolution Equations,
Vol. 13,
Issue. 1,
p.
197.
Bonnans, J. Frédéric
de la Vega, Constanza
and
Dupuis, Xavier
2013.
First- and Second-Order Optimality Conditions for Optimal Control Problems of State Constrained Integral Equations.
Journal of Optimization Theory and Applications,
Vol. 159,
Issue. 1,
p.
1.
Dehghan, Reza
and
Keyanpour, Mohammad
2015.
Optimal control of a system governed by volterra integral equations.
Afrika Matematika,
Vol. 26,
Issue. 5-6,
p.
1111.
Negarchi, N.
and
Nouri, K.
2019.
A New Direct Method for Solving Optimal Control Problem of Nonlinear Volterra–Fredholm Integral Equation via the Müntz–Legendre Polynomials.
Bulletin of the Iranian Mathematical Society,
Vol. 45,
Issue. 3,
p.
917.
Adly, S.
and
Nacry, F.
2019.
An Existence Result for Discontinuous Second-Order Nonconvex State-Dependent Sweeping Processes.
Applied Mathematics & Optimization,
Vol. 79,
Issue. 2,
p.
515.
Zhou, Jianjun
2019.
Delay optimal control and viscosity solutions to associated Hamilton–Jacobi–Bellman equations.
International Journal of Control,
Vol. 92,
Issue. 10,
p.
2263.
Toan, Nguyen Duong
2020.
Optimal Control of Nonclassical Diffusion Equations with Memory.
Acta Applicandae Mathematicae,
Vol. 169,
Issue. 1,
p.
533.
Son, Dang Thanh
and
Toan, Nguyen Duong
2023.
Time Optimal Control Problem of the 2D MHD Equations with Memory.
Journal of Dynamical and Control Systems,
Vol. 29,
Issue. 4,
p.
1323.
Matveeva, Yuliya V.
and
Chigwanda, Marlvin T.
2023.
Modern methods for solving the optimal control problem in economics.
Vestnik of Samara University. Economics and Management,
Vol. 13,
Issue. 4,
p.
97.
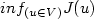 with $J(u):=\int_0^1 L(s,y_u(s),u(s)){\rm d}s+g(y_u(1))$
with $J(u):=\int_0^1 L(s,y_u(s),u(s)){\rm d}s+g(y_u(1))$ 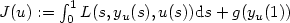 where V is a set of admissible controls and y u is the solution of the Cauchy problem: $\dot{x}(t) =\langle f(.,x(.)), \nu_t \rangle + u(t), t \in (0,1)$
where V is a set of admissible controls and y u is the solution of the Cauchy problem: $\dot{x}(t) =\langle f(.,x(.)), \nu_t \rangle + u(t), t \in (0,1)$ 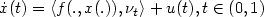 , $x(0) = x_{\rm 0}$
, $x(0) = x_{\rm 0}$ 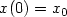 and each $\nu_t$
and each $\nu_t$ 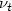 is a nonnegative measure with support in [0,t]. After studying the Cauchy problem, we establish existence of minimizers, optimality conditions (in particular in the form of a nonlocal version of the Pontryagin principle) and prove some regularity results. We also consider the more general case where the control also enters the dynamics in a nonlocal way.
is a nonnegative measure with support in [0,t]. After studying the Cauchy problem, we establish existence of minimizers, optimality conditions (in particular in the form of a nonlocal version of the Pontryagin principle) and prove some regularity results. We also consider the more general case where the control also enters the dynamics in a nonlocal way.