Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-26T14:57:52.214Z Has data issue: false hasContentIssue false
  • English
  • Français

On ergodic problem for Hamilton-Jacobi-Isaacs equations

Published online by Cambridge University Press:  15 September 2005

Piernicola Bettiol
Piernicola Bettiol*
Affiliation:
SISSA/ISAS  via Beirut, 2-4 - 34013 Trieste, Italy; [email protected]
Get access

Abstract

We study the asymptotic behavior of $\lambda v_\lambda$ 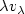as $\lambda\rightarrow 0^+$ 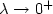, where $v_\lambda$ 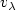is the viscosity solution of the following Hamilton-Jacobi-Isaacs equation (infinite horizon case) \[ \lambda v_\lambda + H(x,Dv_\lambda)=0,\] 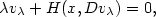with \[H(x,p):=\min_{b\in B}\max_{a \in A} \{-f(x,a,b)\cdot p -l(x,a,b)\}.\] 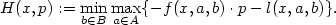We discuss the cases in which the state of the system is required to stay in an n-dimensional torus, called periodic boundary conditions,or in the closure of a bounded connected domain $\Omega\subset{\xR}^n$ 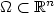with sufficiently smooth boundary. As far as the latter is concerned, we treat boththe case of the Neumann boundary conditions(reflection on the boundary) andthe case of state constraints boundary conditions.Under the uniform approximate controllability assumption of one player, we extendthe uniform convergence result of the value function to a constant as $\lambda\rightarrow 0^+$ 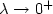to differential games.As far as state constraints boundary conditions are concerned, we give an example where the value function is Hölder continuous.

Keywords

Hamilton-Jacobi-Isaacs equationsviscosity solutionsasymptotic behaviordifferential gamesboundary conditionsergodicity.
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 11 , Issue 4 , October 2005 , pp. 522 - 541
Copyright
© EDP Sciences, SMAI, 2005

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

O. Alvarez and M. Bardi, A general convergence result for singular perturbations of fully nonlinear degenerate parabolic PDEs. University of Padova, Preprint (2002).
Alvarez, O. and Bardi, M., Singular perturbations of nonlinear degenerate parabolic PDEs: a general convergence result. Arch. Rational Mech. Anal. 170 (2003) 17–61. CrossRef
Arisawa, M., Ergodic problem for the Hamilton-Jacobi-Bellman equation I. Ann. Inst. H. Poincaré Anal. Non Linéaire 14 (1997) 415–438. CrossRef
Arisawa, M., Ergodic problem for the Hamilton-Jacobi-Bellman equation II. Ann. Inst. H. Poincaré Anal. Non Linéaire 15 (1998) 1–24. CrossRef
Arisawa, M. and Lions, P.L., Continuity of admissible trajectories for state constraints control problems. Discrete Cont. Dyn. Systems 2 (1996) 297–305.
Arisawa, M. and Lions, P.L., On ergodic stochastic control. Commun. Partial Differ. Equations 23 (1998) 2187–2217. CrossRef
J.P. Aubin and A. Cellina, Differential inclusions. Set-valued maps and viability theory. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences]. Springer-Verlag, Berlin 264 (1984) XIII+342.
M. Bardi and I. Capuzzo-Dolcetta, Optimal control and viscosity solutions of the Hamilton-Jacobi equations. Birkhäuser, Boston (1997).
Bardi, M., Koike, S. and Soravia, P., Pursuit-evasion game with state constraints: dynamic programming and discrete-time approximations. Discrete Cont. Dyn. Systems 6 (2000) 361–380.
G. Barles, Solutions de viscosité des équations de Hamilton-Jacobi. (French) [Viscosity solutions of Hamilton-Jacobi equations.] Mathématiques & Applications [Mathematics & Applications]. Springer-Verlag, Paris 17 (1994) X+194.
P. Bettiol, Weak Solutions in Hamilton-Jacobi and Control Theory. Ph.D. Thesis University of Padova (2002).
P. Bettiol, P. Cardaliaguet and M. Quincampoix, Zero-sum state constrained Differential Games: Victory domains and Existence of value function for Bolza Problem. Preprint SISSA/ISAS Ref. 85/2004/M.
Capuzzo-Dolcetta, I. and Lions, P.L., Hamilton-Jacobi equations with state constraints. Trans. Amer. Math. Soc. 318 (1990) 643–687. CrossRef
Cardaliaguet, P., Quincampoix, M. and Saint-Pierre, P., Pursuit differential games with state constraints. SIAM J. Control Optim. 39 (2001) 1615–1632. CrossRef
Cardaliaguet, P. and Plaskacz, S., Invariant solutions of differential games and Hamilton-Jacobi equations for time-measurable hamiltonians. SIAM J. Control Optim. 38 (2000) 1501–1520. CrossRef
I.P. Cornfeld, S.V. Fomin and Ya.G. Sinaĭ, Ergodic theory. Springer-Verlag, New York (1982). X+486.
M.G. Crandall and P.L. Lions, Condition d'unicité pour les solutions généralisées des équations de Hamilton-Jacobi du premier ordre. (French. English summary.) C. R. Acad. Sci. Paris Sér. I Math. 292 (1981) 183–186.
Crandall, M.G. and Lions, P.L., Viscosity solutions of Hamilton-Jacobi equations. Trans. Amer. Math. Soc. 277 (1983) 1–42. CrossRef
Crandall, M.G., Evans, L.C. and Lions, P.L., Some properties of viscosity solutions of Hamilton-Jacobi equations. Trans. Amer. Math. Soc. 282 (1984) 487–502. CrossRef
L.C. Evans, Partial differential equations. Graduate Studies in Mathematics, 19 AMS, Rhodeisland (1998).
Evans, L.C. and Ishii, H., Differential games and nonlinear first order PDE on bounded domains. Manuscripta Math. 49 (1984) 109–139. CrossRef
Federer, H., Curvature measures. Trans. Amer. Math. Soc. 93 (1959) 418–491. CrossRef
Frankowska, H., Plaskacz, S. and Rzeżuchowski, T., Measurable viability theorems and the Hamilton-Jacobi-Bellman equation. J. Differential Equations 116 (1995) 265–305. CrossRef
Frankowska, H. and Rampazzo, F., Filippov's and Filippov-Ważewski's theorems on closed domains. J. Differential Equations 161 (2000) 449–478. CrossRef
D. Gilbarg and N.S. Trudinger, Elliptic partial differential equations of second order. Reprint of the 1998 edition. Classics in Mathematics. Springer-Verlag, Berlin (2001). XIV+517.
H. Ishii, Lecture notes on viscosity solutions. Brown University, Providence, RI (1988).
Koike, S., On the state constraint problem for differential games. Indiana Univ. Math. J. 44 (1995) 467–487. CrossRef
P.L. Lions, Generalized solutions of Hamilton-Jacobi equations, Research Notes in Mathematics. Pitman (Advanced Publishing Program), Boston, Mass.-London 69 (1982) IV+317.
Lions, P.L., Optimal control of diffusion processes and Hamilton-Jacobi-Bellman equations. I. The dynamic programming principle and applications. Comm. Partial Differ. Equ. 8 (1983) 1101–1174. CrossRef
P.L. Lions, Neumann type boundary conditions for Hamilton-Jacobi equations. Duke Math. J. 52 (1985), 793–820.
Lions, P.L. and Sznitman, A.S., Stochastic differential equations with reflecting boundary conditions. Comm. Pure Appl. Math. 37 (1984) 511–537. CrossRef
Loreti, P. and Tessitore, M.E., Approximation and regularity results on constrained viscosity solutions of Hamilton-Jacobi-Bellman equations. J. Math. Systems Estim. Control 4 (1994) 467–483.
B. Simon, Functional integration and quantum physics. Pure Appl. Math. Academic Press, Inc. [Harcourt Brace Jovanovich, Publishers], New York-London 86 (1979) IX+296.
Soner, M.H., Optimal control with state-space constraint. I. SIAM J. Control Optim. 24 (1986) 552–561. CrossRef