Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-23T23:50:03.008Z Has data issue: false hasContentIssue false
  • English
  • Français

On a semilinear variational problem

Published online by Cambridge University Press:  09 October 2009

Bernd Schmidt
Bernd Schmidt*
Affiliation:
Zentrum Mathematik, Technische Universität München, Boltzmannstr. 3, 85747 Garching, Germany. [email protected]
Get access

Abstract

We provide a detailed analysis of the minimizers of the functional $u \mapsto \int_{\Bbb R^n} |\nabla u|^2 + D \int_{\Bbb R^n} |u|^{\gamma}$ 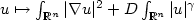, $\gamma \in (0, 2)$ 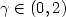, subject to the constraint $\|u\|_{L^2} = 1$ 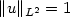. This problem, e.g., describes the long-time behavior of the parabolic Anderson in probability theory or ground state solutions of a nonlinear Schrödinger equation. While existence can be proved with standard methods, we show that the usual uniqueness results obtained with PDE-methods can be considerably simplified by additional variational arguments. In addition, we investigate qualitative properties of the minimizers and also study their behavior near the critical exponent 2.

Keywords

Nonlinear minimum problemparabolic Anderson modelvariational methodsGamma-convergenceground state solutions
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 17 , Issue 1 , January 2011 , pp. 86 - 101
Copyright
© EDP Sciences, SMAI, 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Berestycki, H. and Lions, P.L., Nonlinear scalar field equations I. Existence of a ground state. Arch. Rational Mech. Anal. 82 (1983) 313–345.
Biskup, M. and König, W., Long-time tails in the parabolic Anderson model with bounded potential. Ann. Probab. 29 (2001) 636–682.
A. Braides, Γ-Convergence for Beginners. Oxford University Press, Oxford, UK (2002).
Brother, J.E. and Ziemer, W.P., Minimal rearrangements of Sobolev functions. J. Reine Angew. Math. 384 (1988) 153–179.
Chen, C.C. and Lin, C.S., Uniqueness of the ground state solutions of Δu + f(u) = 0 in $\mathbb{R}^n$ , n ≥ 3. Comm. Partial Diff. Eq. 16 (1991) 1549–1572. CrossRef
Cortazar, C., Elgueta, M. and Felmer, P., On a semilinear elliptic problem in $\mathbb{R}^N$ with a non-Lipschitzian nonlinearity. Adv. Diff. Eq. 1 (1996) 199–218.
Cortazar, C., Elgueta, M. and Felmer, P., Uniqueness of positive solutions of Δu + f(u) = 0 in $\mathbb{R}^n$ , N ≥ 3. Arch. Rational Mech. Anal. 142 (1998) 127–141.
Gärtner, J. and Molchanov, S.A., Parabolic problems for the Anderson model. I. Intermittency and related topics. Comm. Math. Phys. 132 (1990) 613–655. CrossRef
W. König, Große Abweichungen, Techniken und Anwendungen. Vorlesungsskript Universität Leipzig, Germany (2006).
Kwong, M.K., Uniqueness of positive solutions of Δu - u +u p = 0 in $\mathbb{R}^n$ . Arch. Rational Mech. Anal. 105 (1989) 243–266. CrossRef
E.H. Lieb and M. Loss, Analysis, AMS Graduate Studies 14. Second edition, Providence, USA (2001).
Pucci, P., García-Huidobro, M., Manásevich, R. and Serrin, J., Qualitative properties of ground states for singular elliptic equations with weights. Ann. Mat. Pura Appl. 185 (2006) 205–243. CrossRef