Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-23T05:16:28.186Z Has data issue: false hasContentIssue false
  • English
  • Français

The nonlinear membrane model: a Young measureand varifold formulation

Published online by Cambridge University Press:  15 July 2005

Med Lamine Leghmizi ,
Christian Licht  and
Gérard Michaille
Med Lamine Leghmizi
Affiliation:
Centre Universitaire de Médéa, Institut des Sciences de l'Ingénieur, CC 151, Quartier Ain-D'Heb, Médéa (26000), Algeria.
Christian Licht
Affiliation:
Laboratoire de Mécanique et de Génie Civil, UMR-CNRS 5508, Université Montpellier II, Case courier 048, Place Eugène Bataillon, 34095 Montpellier Cedex 5, France.
Gérard Michaille
Affiliation:
ACSIOM et EMIAN, UMR-CNRS 5149, Université Montpellier 2 et CUFR de Nîmes, Case courier 051, Place Eugène Bataillon, 34095 Montpellier Cedex 5, France.
Get access

Abstract

We establish two new formulations of the membrane problem by working in the space of $W^{1,p}_{\Gamma_0}(\Omega,\mathbf R^3)$ 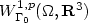-Young measures and $W^{1,p}_{\Gamma_0}(\Omega,\mathbf R^3)$ 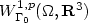-varifolds. The energyfunctional related to these formulations is obtained as a limit of the 3d formulation of the behavior of a thin layer for a suitable variational convergence associated with the narrow convergence of Young measures and with some weak convergence of varifolds. Theinterest of the first formulation is to encode the oscillation informations on the gradients minimizing sequences related to the classicalformulation. The second formulation moreover accounts for concentration effects.

Keywords

MembraneYoung measuresvarifolds.
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 11 , Issue 3 , July 2005 , pp. 449 - 472
Copyright
© EDP Sciences, SMAI, 2005

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

H. Attouch, Variational Convergence for Functions and Operators. Applicable Mathematics Series, Pitman Advanced Publishing Program (1984).
E.J. Balder, Lectures on Young measures theory and its applications in economics. Workshop di Teoria della Misura e Analisi Reale, Grado, 1997, Rend. Istit. Univ. Trieste 31 Suppl. 1 (2000) 1–69.
Bhattacharya, K. and James, R.D., A theory of thin films of martinsitic materials with applications to microactuators. J. Mech. Phys. Solids 47 (1999) 531–576. CrossRef
B. Dacorogna, Direct Methods in the Calculus of Variations. Springer-Verlag, Berlin. Appl. Math. Sciences 78 (1989).
Dal Maso, An introduction to Γ-convergence. Birkäuser, Boston (1993).
Fonseca, I., Müller, S. and Pedregal, P., Analysis of concentration and oscillation effects generated by gradients. SIAM J. Math. Anal. 29 (1998) 736–756. CrossRef
L. Freddi and R. Paroni, The energy density of martensitic thin films via dimension reduction. Rapporto di ricerca n $^\circ9/2003$ del dipartimento di Matematica e Informatica dell'Università di Udine.
Kinderlehrer, D. and Pedregal, P., Characterization of Young measures generated by gradients. Arch. Rational Mech. Anal. 119 (1991) 329–365. CrossRef
H. Le Dret and A. Raoult, The nonlinear membrane model as Variational limit in nonlinear three-dimensional elasticity. J. Math. Pures Appl., IX. Ser. 74 (1995) 549–578.
P. Pedregal, Parametrized measures and variational Principle. Birkhäuser (1997).
Sychev, M.A., A new approach to Young measure theory, relaxation and convergence in energy. Ann. Inst. Henri Poincaé 16 (1999) 773–812. CrossRef
M. Valadier, Young measures. Methods of Nonconvex Analysis, A. Cellina Ed. Springer-Verlag, Berlin. Lect. Notes Math. 1446 (1990) 152–188.
M. Valadier, A course on Young measures. Workshop di Teoria della Misura e Analisi Reale, Grado, September 19–October 2, 1993, Rend. Istit. Mat. Univ. Trieste 26 Suppl. (1994) 349–394