Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-23T18:02:19.418Z Has data issue: false hasContentIssue false
  • English
  • Français

Necessary conditions for weak lower semicontinuityon domains with infinite measure

Published online by Cambridge University Press:  21 April 2009

Stefan Krömer
Stefan Krömer*
Affiliation:
Department of Mathematical Sciences, Carnegie Mellon University, Pittsburgh, PA 15213-3890, USA. [email protected]
Get access

Abstract

We derive sharp necessary conditions for weak sequential lower semicontinuity of integral functionals on Sobolev spaces, with an integrand which only depends on the gradient of a scalar field over a domain in ${\mathbb R}^N$ 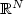. An emphasis is put on domains with infinite measure, and the integrand is allowed to assume the value $+\infty$ .

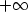Keywords

Scalar integral functionalsweak lower semicontinuitynecessary conditions
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 16 , Issue 2 , April 2010 , pp. 457 - 471
Copyright
© EDP Sciences, SMAI, 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

B. Dacorogna, Direct methods in the calculus of variations, Applied Mathematical Sciences 78. Springer, Berlin etc. (1989).
I. Fonseca and G. Leoni, Modern Methods in the Calculus of Variations: Lp Spaces, Springer Monographs in Mathematics. Springer, New York (2007).
E. Giusti, Direct methods in the calculus of variations. World Scientific, Singapore (2003).
Gustin, W., On the interior of the convex hull of an Euclidean set. Bull. Am. Math. Soc. 53 (1947) 299–301. CrossRef
V.G. Maz'ya, Sobolev spaces. Springer-Verlag, Berlin etc. (1985).
Yu.S. Nikol'skij, Integral estimates for differentiable functions on unbounded domains. Proc. Steklov Inst. Math. 170 (1987) 267–283. Translation from Tr. Mat. Inst. Steklova 170 (1984) 233–247 (Russian).