Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-22T21:06:24.070Z Has data issue: false hasContentIssue false
  • English
  • Français

Monotonicity properties of minimizers and relaxationfor autonomous variational problems

Published online by Cambridge University Press:  24 March 2010

Giovanni Cupini  and
Cristina Marcelli
Giovanni Cupini
Affiliation:
Dipartimento di Matematica, Università di Bologna, Piazza di Porta S.Donato 5, 40126 Bologna, Italy. [email protected]
Cristina Marcelli
Affiliation:
Dipartimento di Scienze Matematiche, Università Politecnica delle Marche, Via Brecce Bianche, 60131 Ancona, Italy. [email protected]
Get access

Abstract

We consider the following classical autonomous variational problem

\[ \textrm{minimize\,} \left\{F(v)=\int_a^b f(v(x),v'(x))\ \dx\,:\,v\in AC([a,b]), \;v(a)=\alpha,\; v(b)=\beta\right\},\]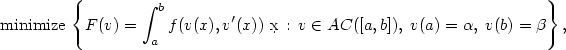

where the Lagrangian f is possibly neither continuous, nor convex, nor coercive.We prove a monotonicity property of the minimizers stating that they satisfy the maximum principle or the minimum one. By virtue of such a property, applying recent results concerning constrained variational problems, we derive a relaxation theorem, the DuBois-Reymond necessary condition and some existenceor non-existence criteria.

Keywords

Nonconvex variational problemsautonomous variationalproblemsexistence of minimizersDuBois-Reymond necessaryconditionrelaxation
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 17 , Issue 1 , January 2011 , pp. 222 - 242
Copyright
© EDP Sciences, SMAI, 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ambrosio, L., Ascenzi, O. and Buttazzo, G., Lipschitz regularity for minimizers of integral functionals with highly discontinuous integrands. J. Math. Anal. Appl. 142 (1989) 301–316. CrossRef
V.I. Bogachev, Measure Theory, Volume I. Springer-Verlag, Berlin, Germany (2007).
Botteron, B. and Dacorogna, B., Existence of solutions for a variational problem associated to models in optimal foraging theory. J. Math. Anal. Appl. 147 (1990) 263–276. CrossRef
Botteron, B. and Dacorogna, B., Existence and nonexistence results for noncoercive variational problems and applications in ecology. J. Differ. Equ. 85 (1990) 214–235. CrossRef
B. Botteron and P. Marcellini, A general approach to the existence of minimizers of one-dimensional noncoercive integrals of the calculus of variations. Ann. Inst. Henri Poincaré, Anal. non linéaire 8 (1991) 197–223.
Celada, P. and Perrotta, S., Existence of minimizers for nonconvex, noncoercive simple integrals. SIAM J. Control Optim. 41 (2002) 1118–1140. CrossRef
Cellina, A., The classical problem of the calculus of variations in the autonomous case: relaxation and lipschitzianity of solutions. Trans. Amer. Math. Soc. 356 (2004) 415–426. CrossRef
A. Cellina and A. Ferriero, Existence of Lipschitzian solutions to the classical problem of the calculus of variations in the autonomous case. Ann. Inst. Henri Poincaré, Anal. non linéaire 20 (2003) 911–919.
Cellina, A., Treu, G. and Zagatti, S., On the minimum problem for a class of non-coercive functionals. J. Differ. Equ. 127 (1996) 225–262. CrossRef
L. Cesari, Optimization: theory and applications. Springer-Verlag, New York, USA (1983).
Clarke, F.H., An indirect method in the calculus of variations. Trans. Amer. Math. Soc. 336 (1993) 655–673. CrossRef
Cupini, G., Guidorzi, M. and Marcelli, C., Necessary conditions and non-existence results for autonomous nonconvex variational problems. J. Differ. Equ. 243 (2007) 329–348. CrossRef
B. Dacorogna, Direct methods in the Calculus of Variations, Applied Mathematical Sciences 78. Second edition, Springer, Berlin, Germany (2008).
Dal Maso, G. and Frankowska, H., Autonomous integral functionals with discontinuous nonconvex integrands: Lipschitz regularity of minimizers, DuBois-Reymond necessary conditions, and Hamilton-Jacobi equations. Appl Math Optim. 48 (2003) 39–66.
E. De Giorgi, G. Buttazzo and G. Dal Maso, On the lower semicontinuity of certain integral functionals. Atti Accad. Naz. Lincei, VIII. Ser. 74 (1983) 274–282.
I. Ekeland and R. Temam, Convex analysis and variational problems, Studies in Mathematics and its Applications 1. North Holland, Amsterdam, The Netherlands (1976).
Fusco, N., Marcellini, P. and Ornelas, A., Existence of minimizers for some nonconvex one-dimensional integrals. Port. Math. 55 (1998) 167–185.
O.A. Ladyzhenskaya and N.N. Ural'tseva, Linear and Quasilinear Elliptic Equations, Mathematics in Science and Engineering 46. Academic Press, New York-London (1968).
Marcelli, C., Variational problems with nonconvex, noncoercive, highly discontinuous integrands: characterization and existence of minimizers. SIAM J. Control Optim. 40 (2002) 1473–1490. CrossRef
Marcelli, C., Necessary and sufficient conditions for optimality of nonconvex, noncoercive autonomous variational problems with constraints. Trans. Amer. Math. Soc. 360 (2008) 5201–5227. CrossRef
Marcellini, P., Alcune osservazioni sull'esistenza del minimo di integrali del calcolo delle variazioni senza ipotesi di convessità. Rend. Mat. Appl. 13 (1980) 271–281.
Ornelas, A., Existence of scalar minimizers for nonconvex simple integrals of sum type. J. Math. Anal. Appl. 221 (1998) 559–573. CrossRef
Ornelas, A., Existence and regularity for scalar minimizers of affine nonconvex simple integrals. Nonlinear Anal. 53 (2003) 441–451. CrossRef
Ornelas, A., Existence of scalar minimizers for simple convex integrals with autonomous Lagrangian measurable on the state variable. Nonlinear Anal. 67 (2007) 2485–2496. CrossRef
Raymond, J.P., Existence and uniqueness results for minimization problems with nonconvex functionals. J. Optim. Theory Appl. 82 (1994) 571–592. CrossRef