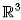For a given U(1)-bundle E over M = $\lambda _{2}$ \{x1, ..., xn }, where the xi are n distinct points of $\lambda _{2}$ 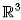, we minimise the U(1)-Higgs action and we make an asymptotic analysis of the minimizers when the coupling constant tends to infinity. We prove that the curvature (= magnetic field) converges to a limiting curvature that we give explicitely and which is singular along line vortices which connect the xi . This work is the three dimensional equivalent of previous works in dimension two (see [3] and [4]). The results presented here were announced in [12].