Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-19T06:05:41.926Z Has data issue: false hasContentIssue false
  • English
  • Français

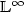Linearization techniques for $\mathbb{L}^{\infty}$See PDF-control problemsand dynamic programming principles in classical and $\mathbb{L}^{\infty}$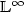See PDF-control problems

Published online by Cambridge University Press:  17 August 2011

Dan Goreac  and
Oana-Silvia Serea
Dan Goreac
Affiliation:
UniversitéParis-Est Marne-la-Vallée, LAMA, UMR8050, 5, boulevard Descartes, Cité Descartes, Champs-sur-Marne, 77454 Marne-la-Vallée, France
Oana-Silvia Serea
Affiliation:
Université de Perpignan, LAMPS, 52, av. Paul Alduy, 66860 Perpignan and École Polytechnique, CMAP, Route de Saclay, 91128 Palaiseau Cedex, France. [email protected]
Get access

Abstract

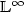The aim of the paper is to provide a linearization approach to the $\mathbb{L}^{\infty}$See PDF-control problems. We begin by proving a semigroup-type behaviour of the set of constraints appearing in the linearized formulation of (standard) control problems. As a byproduct we obtain a linear formulation of the dynamic programming principle. Then, we use the $\mathbb{L}^{p}$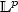See PDF approach and the associated linear formulations. This seems to be the most appropriate tool for treating $\mathbb{L}^{\infty}$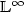See PDF problems in continuous and lower semicontinuous setting.

Keywords

Dynamic programming principleessential supremumHJ equationsoccupational measures$\mathbb{L}^{p}$See PDF approximations
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 18 , Issue 3 , July 2012 , pp. 836 - 855
Copyright
© EDP Sciences, SMAI, 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

M. Bardi and I. Capuzzo-Dolcetta, Optimal control and viscosity solutions of Hamilton-Jacobi-Bellman equations. Systems and Control : Foundations and Applications, Birkhäuser, Boston (1997).
G. Barles, Solutions de viscosity des equations de Hamilton-Jacobi (Viscosity solutions of Hamilton-Jacobi equations), Mathematiques & Applications (Paris) 17. Springer-Verlag, Paris (1994).
Barles, G. and Jakobsen, E.R., On the convergence rate of approximation schemes for Hamilton-Jacobi-Bellman equations. ESAIM : M2AN 36 (2002) 33–54. Google Scholar
Barron, E.N. and Ishii, H., The bellman equation for minimizing the maximum cost. Nonlinear Anal. 13 (1989) 1067–1090. Google Scholar
Barron, E.N. and Jensen, R., Semicontinuous viscosity solutions for Hamilton-Jacobi equations with convex Hamiltonians. Commun. Partial Differ. Equ. 15 (1990) 1713–1742. Google Scholar
Bhatt, A.G. and Borkar, V.S., Occupation measures for controlled markov processes : Characterization and optimality. Ann. Probab. 24 (1996) 1531–1562. Google Scholar
Borkar, V. and Gaitsgory, V., Averaging of singularly perturbed controlled stochastic differential equations. Appl. Math. Optim. 56 (2007) 169–209. Google Scholar
Buckdahn, R., Goreac, D. and Quincampoix, M., Stochastic optimal control and linear programming approach. Appl. Math. Optim. 63 (2011) 257–276. Google Scholar
Fleming, W.H. and Vermes, D., Convex duality approach to the optimal control of diffusions. SIAM J. Control Optim. 27 (1989) 1136–1155. Google Scholar
Frankowska, H., Lower semicontinuous solutions of Hamilton-Jacobi-Bellman equations. SIAM J. Control Optim. 31 (1993) 257–272. Google Scholar
Gaitsgory, V. and Quincampoix, M., Linear programming approach to deterministic infinite horizon optimal control problems with discounting. SIAM J. Control Optim. 48 (2009) 2480–2512. Google Scholar
Gaitsgory, V. and Rossomakhine, S., Linear programming approach to deterministic long run average problems of optimal control. SIAM J. Control Optim. 44 (2006) 2006–2037. Google Scholar
Goreac, D. and Serea, O.S., Discontinuous control problems for non-convex dynamics and near viability for singularly perturbed control systems. Nonlinear Anal. 73 (2010) 2699–2713. Google Scholar
Goreac, D. and Serea, O.S., Mayer and optimal stopping stochastic control problems with discontinuous cost. J. Math. Anal. Appl. 380 (2011) 327–342. Google Scholar
Krylov, N.V., On the rate of convergence of finte-difference approximations for bellman’s equations with variable coefficients. Probab. Theory Relat. Fields 117 (2000) 1–16. Google Scholar
Plaskacz, S. and Quincampoix, M., Value-functions for differential games and control systems with discontinuous terminal cost. SIAM J. Control Optim. 39 (2001) 1485–1498. Google Scholar
Quincampoix, M. and Serea, O.S., The problem of optimal control with reflection studied through a linear optimization problem stated on occupational measures. Nonlinear Anal. 72 (2010) 2803–2815. Google Scholar
Serea, O.S., Discontinuous differential games and control systems with supremum cost. J. Math. Anal. Appl. 270 (2002) 519–542. Google Scholar
Serea, O.S., On reflecting boundary problem for optimal control. SIAM J. Control Optim. 42 (2003) 559–575. Google Scholar
A.I. Subbotin, Generalized solutions of first-order PDEs, The dynamical optimization perspective. Birkhäuser, Basel (1994).
C. Villani, Optimal Transport : Old and New. Springer (2009).
Vinter, R., Convex duality and nonlinear optimal control. SIAM J. Control Optim. 31 (1993) 518–538. Google Scholar