Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-25T03:09:04.086Z Has data issue: false hasContentIssue false
  • English
  • Français

Junction of elastic plates and beams

Published online by Cambridge University Press:  26 July 2007

Antonio Gaudiello ,
Régis Monneau ,
Jacqueline Mossino ,
François Murat  and
Ali Sili
Antonio Gaudiello
Affiliation:
Dipartimento di Automazione, Elettromagnetismo, Ingegneria dell'Informazione e Matematica Industriale, Università di Cassino, via G. Di Biasio 43, 03043 Cassino (FR), Italia; [email protected]
Régis Monneau
Affiliation:
CERMICS, École Nationale des Ponts et Chaussées, 6 et 8 Avenue Blaise Pascal, Cité Descartes, 77455 Champs-sur-Marne Cedex 2, France; [email protected]
Jacqueline Mossino
Affiliation:
CMLA, École Normale Supérieure de Cachan, 61 Avenue du Président Wilson, 94235 Cachan Cedex, France; [email protected]
François Murat
Affiliation:
Laboratoire Jacques-Louis Lions, Université Pierre et Marie Curie, Boîte courrier 187, 75252 Paris Cedex 05, France; [email protected]
Ali Sili
Affiliation:
Département de Mathématiques, Université de Toulon et du Var, BP 132, 83957 La Garde Cedex, France; [email protected]
Get access

Abstract

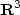We consider the linearized elasticity system in a multidomain of ${\bf R}^3$ . This multidomain is the union of a horizontal plate with fixed cross section and small thickness ε, and of a vertical beam with fixed height and small cross section of radius $r^{\varepsilon}$ 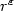. The lateral boundary of the plate and the top of the beam are assumed to be clamped. When ε and $r^{\varepsilon}$ 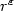tend to zero simultaneously, with $r^{\varepsilon}\gg\varepsilon^2$ 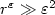, we identify the limit problem. This limit problem involves six junction conditions.

Keywords

Junctionsthin structuresplatesbeamslinear elasticityasymptotic analysis
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 13 , Issue 3 , July 2007 , pp. 419 - 457
Copyright
© EDP Sciences, SMAI, 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acerbi, E., Buttazzo, G. and Percivale, D., A variational definition of the strain energy for an elastic string. J. Elasticity 25 (1991) 137–148. CrossRef
D.R. Adams and L.I. Hedberg, Fonctions Spaces and Potential Theory. Springer Verlag, Berlin (1996).
Anzellotti, G., Baldo, S. and Percivale, D., Dimension reduction in variational problems, asymptotic development in $\Gamma$ -convergence and thin structures in elasticity. Asymptot. Anal. 9 (1994) 61–100.
Caillerie, D., Thin elastic and periodic plates. Math. Methods Appl. Sci. 6 (1984) 159–191. CrossRef
P.G. Ciarlet, Plates and Junctions in Elastic Multi-Structures: An Asymptotic Analysis. Masson, Paris (1990).
P.G. Ciarlet, Mathematical Elasticity, Volume II: Theory of Plates. North-Holland, Amsterdam (1997).
Ciarlet, P.G. and Destuynder, P., A justification of the two-dimensional linear plate model. J. Mécanique 18 (1979) 315–344.
Cimetière, A., Geymonat, G., Le Dret, H., Raoult, A., Tutek, Z., Asymptotic theory and analysis for displacements and stress distribution in nonlinear elastic straight slender rods. J. Elasticity 19 (1988) 111–161. CrossRef
D. Cioranescu and J. Saint Jean Paulin, Homogenization of Reticulated Structures. Springer-Verlag, New York (1999).
Dauge, M. and Gruais, I., Asymptotics of arbitrary order for a thin elastic clamped plate, I: Optimal error estimates. Asymptot. Anal. 13 (1996) 167–197.
Friesecke, G., James, R.D. and Müller, S., A theorem on geometric rigidity and the derivation of nonlinear plate theory from three-dimensional elasticity. Comm. Pure Appl. Math. 55 (2002) 1461–1506. CrossRef
Friesecke, G., James, R.D. and Müller, S., A hierarchy of plate models derived from nonlinear elasticity by gamma-convergence. Arch. Rat. Mech. Anal. 180 (2006) 183–236. CrossRef
Gaudiello, A., Gustafsson, B., Lefter, C. and Mossino, J., Asymptotic analysis of a class of minimization problems in a thin multidomain. Calc. Var. Part. Diff. Eq. 15 (2002) 181–201. CrossRef
Gaudiello, A., Gustafsson, B., Lefter, C. and Mossino, J., Asymptotic analysis for monotone quasilinear problems in thin multidomains. Diff. Int. Eq. 15 (2002) 623–640.
Gaudiello, A., Monneau, R., Mossino, J., Murat, F. and Sili, A., On the junction of elastic plates and beams. C.R. Acad. Sci. Paris Sér. I 335 (2002) 717–722. CrossRef
Gaudiello, A. and Zappale, E., Junction in a thin multidomain for a fourth order problem. M3AS: Math. Models Methods Appl. Sci. 16 (2006) 1887–1918.
Gruais, I., Modélisation de la jonction entre une plaque et une poutre en élasticité linéarisée. RAIRO: Modél. Math. Anal. Numér. 27 (1993) 77–105.
Gruais, I., Modeling of the junction between a plate and a rod in nonlinear elasticity. Asymptotic Anal. 7 (1993) 179–194.
Kozlov, V.A., Ma'zya, V.G. and Movchan, A.B., Asymptotic representation of elastic fields in a multi-structure. Asymptot. Anal. 11 (1995) 343–415.
H. Le Dret, Problèmes Variationnels dans les Multi-domaines: Modélisation des Jonctions et Applications. Masson, Paris (1991).
Le Dret, H., Convergence of displacements and stresses in linearly elastic slender rods as the thickness goes to zero. Asymptot. Anal. 10 (1995) 367–402.
Le Dret, H. and Raoult, A., The nonlinear membrane model as variational limit of nonlinear three-dimensional elasticity. J. Math. Pures Appl. 74 (1995) 549–578.
Le Dret, H. and Raoult, A., The membrane shell model in nonlinear elasticity: a variational asymptotic derivation. J. Nonlinear Sci. 6 (1996) 59–84. CrossRef
R. Monneau, F. Murat and A. Sili, Error estimate for the transition 3d-1d in anisotropic heterogeneous linearized elasticity. To appear.
Mora, M.G. and Müller, S., Derivation of the nonlinear bending-torsion theory for inextensible rods by $\Gamma$ -convergence. Calc. Var. Part. Diff. Eq. 18 (2003) 287–305. CrossRef
Mora, M.G. and Müller, S., A nonlinear model for inextensible rods as a low energy $\Gamma$ -limit of three-dimensional nonlinear elasticity. Ann. Inst. H. Poincaré Anal. Non Linéaire 21 (2004) 271–293.
Murat, F. and Sili, A., Comportement asymptotique des solutions du sytème de l'élasticité linéarisée anisotrope hétérogène dans des cylindres minces. C.R. Acad. Sci. Paris Sér. I 328 (1999) 179–184. CrossRef
F. Murat and A. Sili, Anisotropic, heterogeneous, linearized elasticity problems in thin cylinders. To appear.
O.A. Oleinik, A.S. Shamaev and G.A. Yosifian, Mathematical Problems in Elasticity and Homogenization. North-Holland, Amsterdam (1992).
Percivale, D., Thin elastic beams: the variational approach to St. Venant's problem. Asymptot. Anal. 20 (1999) 39–60.
L. Trabucho and J.M. Viano, Mathematical Modelling of Rods, Handbook of Numerical Analysis 4. North-Holland, Amsterdam (1996).