Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-10T20:39:45.896Z Has data issue: false hasContentIssue false
  • English
  • Français

Higher-order phase transitions with line-tension effect

Published online by Cambridge University Press:  23 April 2010

Bernardo Galvão-Sousa
Bernardo Galvão-Sousa*
Affiliation:
Department of Mathematics and Statistics, McMaster University, Hamilton ON L8S 4K1, Canada. [email protected]
Get access

Abstract

The behavior of energy minimizers at the boundary of the domain is of great importance in the Van de Waals-Cahn-Hilliard theory for fluid-fluid phase transitions, since it describes the effect of the container walls on the configuration of the liquid. This problem, also known as the liquid-drop problem, was studied by Modica in [Ann. Inst. Henri Poincaré, Anal. non linéaire 4 (1987) 487–512], and in a different form by Alberti et al. in [Arch. Rational Mech. Anal. 144 (1998) 1–46] for a first-order perturbation model.This work shows that using a second-order perturbation Cahn-Hilliard-type model, the boundary layer is intrinsically connected with the transition layer in the interior of the domain. Precisely, considering the energies

$\[{\cal F}_{\varepsilon}(u) := \varepsilon^{3} \int_{\Omega} |D^{2}u|^{2} + \frac{1}{\varepsilon} \int_{\Omega} W (u) + \lambda_{\varepsilon} \int_{\partial \Omega} V(Tu),\]$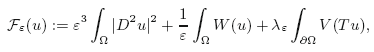

where u is a scalar density function and W and V are double-well potentials, the exact scaling law is identified in the critical regime, when $\varepsilon\lambda_{\varepsilon}^{\frac{2}{3}} \sim 1$.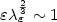

Keywords

Gamma limitfunctions of bounded variationsfunctions of bounded variations on manifoldsphase transitions
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 17 , Issue 3 , July 2011 , pp. 603 - 647
Copyright
© EDP Sciences, SMAI, 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

R. Adams, Sobolev Spaces. Academic Press (1975).
Alberti, G., Bouchitté, G. and Seppecher, P., Phase transition with the line tension effect. Arch. Rational Mech. Anal. 144 (1998) 1–46. CrossRef
L. Ambrosio, N. Fusco and D. Pallara, Functions of Bounded Variation and Free Discontinuity Problems. Oxford Clarendon Press, Oxford (2000).
J. Ball, A version of the fundamental theorem for Young measures, in PDEs and continuum models of phase transitions (Nice, 1988), Lecture Notes in Phys. 344, Springer, Berlin (1989) 207–215.
Choksi, R. and Kohn, R., Bounds on the micromagnetic energy of a uniaxial ferromagnet. Comm. Pure Appl. Math. 51 (1998) 259–289. 3.0.CO;2-9>CrossRef
Choksi, R., Kohn, R. and Otto, F., Domain branching in uniaxial ferromagnets: a scaling law for the minimum energy. Comm. Math. Phys. 201 (1999) 61–79. CrossRef
Choksi, R., Kohn, R. and Otto, F., Energy minimization and flux domain structure in the intermediate state of a type-I superconductor. J. Nonlinear Sci. 14 (2004) 119–171. CrossRef
Choksi, R., Conti, S., Kohn, R. and Otto, F., Ground state energy scaling laws during the onset and destruction of the intermediate state in a type I superconductor. Comm. Pure Appl. Math. 61 (2008) 595–626. CrossRef
Conti, S., Fonseca, I. and Leoni, G., A Γ-convergence result for the two-gradient theory of phase transitions. Comm. Pure Applied Math. 55 (2002) 857–936. CrossRef
G. Dal Maso, An Introduction to Γ-Convergence. Birkhäuser (1993).
E. DiBenedetto, Real Analysis. Birkhäuser (2002).
L. Evans and R. Gariepy, Measure Theory and fine Properties of Functions. CRC Press (1992).
I. Fonseca and G. Leoni, Modern methods in the calculus of variations: Lp spaces, Springer Monographs in Mathematics. Springer (2007).
Fonseca, I. and Mantegazza, C., Second order singular perturbation models for phase transitions. SIAM J. Math. Anal. 31 (2000) 1121–1143. CrossRef
Gagliardo, E., Ulteriori prorietà di alcune classi di funzioni in più variabili. Ric. Mat. 8 (1959) 24–51.
A. Garroni and G. Palatucci, A singular perturbation result with a fractional norm, in Variational problems in materials science, Progr. Nonlinear Differential Equations Appl. 68, Birkhäuser, Basel (2006) 111–126.
E. Giusti, Minimal Surfaces and Functions of Bounded Variation. Birkhäuser (1984).
E. Hebey, Nonlinear Analysis on Manifolds: Sobolev Spaces and Inequalities. AMS/CIMS (1999).
Miranda, M., Pallara, D., Paronetto, F. and Preunkert, M., Heat semigroup and functions of bounded variation on Riemannian manifolds. J. Reine Angew. Math. 613 (2007) 99–119.
Modica, L., The gradient theory of phase transitions and the minimal interface criterion. Arch. Rational Mech. Anal. 98 (1987) 123–142. CrossRef
L. Modica, The gradient theory of phase transitions with boundary contact energy. Ann. Inst. Henri Poincaré, Anal. non linéaire 4 (1987) 487–512. CrossRef
Modica, L. and Mortola, S., Un esempio de Γ --convergenza. Boll. Un. Mat. Ital. B 14 (1977) 285–299.
S. Müller, Variational models for microstructure and phase transitions, in Calculus of variations and geometric evolution problems (Cetraro, 1996), Lecture Notes in Math. 1713, Springer (1999) 85–210.
Nirenberg, L., An extended interpolation inequality. Ann. Sc. Normale Pisa - Scienze fisiche e matematiche 20 (1966) 733–737.
E. Stein, Singular Integrals and Differentiability Properties of Functions. Princeton University Press (1970).
L. Tartar, Compensated compactness and applications to partial differential equations, in Nonlinear analysis and mechanics: Heriot-Watt Symposium IV, Res. Notes in Math. 39, Pitman, Boston (1979) 136–212.
W. Ziemer, Weakly differentiable functions – Sobolev spaces and functions of bounded variation, Graduate Texts in Mathematics 120. Springer-Verlag, New York (1989).