The energy in a square membrane Ω subject to constant viscous dampingon a subset $\omega\subset \Omega$ 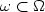decays exponentially in timeas soon as ωsatisfies a geometrical condition known as the “Bardos-Lebeau-Rauch” condition. The rate $\tau(\omega)$ 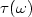of this decay satisfies $\tau(\omega)= 2 \min( -\mu(\omega),g(\omega))$ 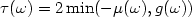(see Lebeau [Math.Phys. Stud.19 (1996) 73–109]). Here $\mu(\omega)$ 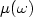denotes the spectral abscissa of thedamped wave equation operator and  $g(\omega)$ 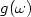is a number called the geometrical quantity of ω and defined as follows.A ray in Ω is the trajectory generated by thefree motion of a mass-point in Ω subject to elastic reflections on theboundary. These reflections obey the law of geometrical optics.The geometrical quantity $g(\omega)$ 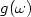is then defined as the upper limit (large timeasymptotics) of the average trajectory length. We give here an algorithm to compute explicitly $g(\omega)$ 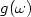when ωis a finite union of squares.