Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Babadjian, Jean-François
and
Francfort, Gilles A.
2005.
Spatial heterogeneity in 3D-2D dimensional reduction.
ESAIM: Control, Optimisation and Calculus of Variations,
Vol. 11,
Issue. 1,
p.
139.
Braides, Andrea
2006.
Vol. 3,
Issue. ,
p.
101.
Fonseca, Irene
2008.
Classical and Advanced Theories of Thin Structures.
Vol. 503,
Issue. ,
p.
205.
Babadjian, Jean-François
2008.
Lower Semicontinuity of Quasi-convex Bulk Energies in SBV and Integral Representation in Dimension Reduction.
SIAM Journal on Mathematical Analysis,
Vol. 39,
Issue. 6,
p.
1921.
Bocea, Marian
2008.
A justification of the theory of martensitic thin films in the absence of an interfacial energy.
Journal of Mathematical Analysis and Applications,
Vol. 342,
Issue. 1,
p.
485.
Fonseca, Irene
2008.
Classical and Advanced Theories of Thin Structures.
Vol. 503,
Issue. ,
p.
235.
Carita, Graça
and
Zappale, Elvira
2012.
3D–2D dimensional reduction for a nonlinear optimal design problem with perimeter penalization.
Comptes Rendus. Mathématique,
Vol. 350,
Issue. 23-24,
p.
1011.
Marohnić, Maroje
and
Velčić, Igor
2015.
Homogenization of bending theory for plates; the case of oscillations in the direction of thickness.
Communications on Pure and Applied Analysis,
Vol. 14,
Issue. 6,
p.
2151.
Kreisbeck, Carolin
and
Krömer, Stefan
2016.
Heterogeneous Thin Films: Combining Homogenization and Dimension Reduction with Directors.
SIAM Journal on Mathematical Analysis,
Vol. 48,
Issue. 2,
p.
785.
Kozarzewski, Piotr Antoni
and
Zappale, Elvira
2017.
Orlicz equi-integrability for scaled gradients.
Journal of Elliptic and Parabolic Equations,
Vol. 3,
Issue. 1-2,
p.
1.
Velčić, Igor
2017.
On the general homogenization of von Kármán plate equations from three-dimensional nonlinear elasticity.
Analysis and Applications,
Vol. 15,
Issue. 01,
p.
1.
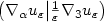 bounded in $L^p (\Omega;
\mathbb{R}^9 ), \ 1 < p < +\infty .$
bounded in $L^p (\Omega;
\mathbb{R}^9 ), \ 1 < p < +\infty .$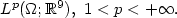 Here it is shown that, up to a
subsequence, $u_\varepsilon$
Here it is shown that, up to a
subsequence, $u_\varepsilon$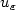 may be decomposed as $w_\varepsilon+ z_\varepsilon,$
may be decomposed as $w_\varepsilon+ z_\varepsilon,$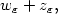 where $z_\varepsilon$
where $z_\varepsilon$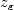 carries all the concentration effects, i.e.$\left\{ \left| \left( \nabla _{\alpha }w_\varepsilon| \frac{1}{\varepsilon
}\nabla _3 w_\varepsilon\right) \right| ^{p} \right\} $
carries all the concentration effects, i.e.$\left\{ \left| \left( \nabla _{\alpha }w_\varepsilon| \frac{1}{\varepsilon
}\nabla _3 w_\varepsilon\right) \right| ^{p} \right\} $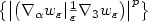 is
equi-integrable, and $w_\varepsilon$
is
equi-integrable, and $w_\varepsilon$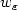 captures the oscillatory behavior,
i.e.$z_\varepsilon\to 0$
captures the oscillatory behavior,
i.e.$z_\varepsilon\to 0$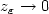 in measure. In addition, if $\{ u_\varepsilon\} $
in measure. In addition, if $\{ u_\varepsilon\} $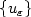 is
a recovering sequence then $z_\varepsilon= z_\varepsilon(x_\alpha )$
is
a recovering sequence then $z_\varepsilon= z_\varepsilon(x_\alpha )$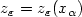 nearby
$\partial \Omega.$
nearby
$\partial \Omega.$