Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-09T08:23:02.888Z Has data issue: false hasContentIssue false
  • English
  • Français

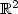Entire solutions in ${\mathbb{R}}^{2}$ for a class of Allen-Cahn equations

Published online by Cambridge University Press:  15 September 2005

Francesca Alessio  and
Piero Montecchiari
Francesca Alessio
Affiliation:
Dipartimento di Scienze Matematiche, Università Politecnica delle Marche, via Brecce Bianche, 60131 Ancona, Italy; [email protected];[email protected]
Piero Montecchiari
Affiliation:
Dipartimento di Scienze Matematiche, Università Politecnica delle Marche, via Brecce Bianche, 60131 Ancona, Italy; [email protected];[email protected]
Get access

Abstract

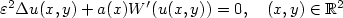We consider a class ofsemilinear elliptic equations of the form 15.7cm - $\varepsilon^{2}\Delta u(x,y)+a(x)W'(u(x,y))=0,\quad (x,y)\in{\mathbb{R}}^{2}$ where $\varepsilon>0$ 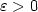, $a:{\mathbb{R}}\to{\mathbb{R}}$ 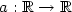is a periodic, positive function and $W:{\mathbb{R}}\to{\mathbb{R}}$ 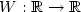is modeled on the classical two well Ginzburg-Landaupotential $W(s)=(s^{2}-1)^{2}$ 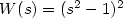. We look for solutions to ([see full textsee full text])which verify theasymptotic conditions $u(x,y)\to\pm 1$ 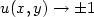as $x\to\pm\infty$ 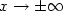uniformly with respect to $y\in{\mathbb{R}}$ 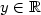.We show via variationalmethods that if ε is sufficiently small and a is not constant, then ([see full textsee full text])admits infinitely many of such solutions, distinct up to translations, which do not exhibit one dimensional symmetries.

Keywords

Heteroclinicsolutionselliptic equationsvariationalmethods.
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 11 , Issue 4 , October 2005 , pp. 633 - 672
Copyright
© EDP Sciences, SMAI, 2005

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alama, S., Bronsard, L. and Gui, C., Stationary layered solutions in $\mathbb{R}^{2}$ for an Allen-Cahn system with multiple well potential. Calc. Var. 5 (1997) 359–390. CrossRef
Alberti, G., Ambrosio, L. and Cabré, X., On a long-standing conjecture of E. De Giorgi: Symmetry in 3D for general nonlinearities and a local minimality property. Acta Appl. Math. 65 (2001) 9–33. CrossRef
Alessio, F., Jeanjean, L. and Montecchiari, P., Stationary layered solutions in $\mathbb{R}^{2}$ for a class of non autonomous Allen-Cahn equations. Calc. Var. Partial Differ. Equ. 11 (2000) 177–202. CrossRef
Alessio, F., Jeanjean, L. and Montecchiari, P., Existence of infinitely many stationary layered solutions in $\mathbb{R}^{2}$ for a class of periodic Allen Cahn Equations. Commun. Partial Differ. Equ. 27 (2002) 1537–1574. CrossRef
Ambrosio, L. and Cabre, X., Entire solutions of semilinear elliptic equations in $\mathbb{R}^{3}$ and a conjecture of De Giorgi. J. Am. Math. Soc. 13 (2000) 725–739. CrossRef
Bargert, V., On minimal laminations on the torus. Ann. Inst. H. Poincaré Anal. Nonlinéaire 6 (1989) 95–138. CrossRef
Barlow, M.T., Bass, R.F. and Gui, C., The Liouville property and a conjecture of De Giorgi. Comm. Pure Appl. Math. 53 (2000) 1007–1038. 3.0.CO;2-U>CrossRef
Berestycki, H., Hamel, F. and Monneau, R., One-dimensional symmetry for some bounded entire solutions of some elliptic equations. Duke Math. J. 103 (2000) 375–396.
E. De Giorgi, Convergence problems for functionals and operators, in Proc. Int. Meeting on Recent Methods in Nonlinear Analysis. Rome, E. De Giorgi et al. Eds. (1978).
A. Farina, Symmetry for solutions of semilinear elliptic equations in $\mathbb{R}^{N}$ and related conjectures. Ricerche Mat. (in memory of Ennio De Giorgi) 48 (1999) 129–154.
Ghoussoub, N. and Gui, C., On a conjecture of De Giorgi and some related problems. Math. Ann. 311 (1998) 481–491. CrossRef
Moser, J., Minimal solutions of variational problem on a torus. Ann. Inst. H. Poincaré Anal. NonLinéaire 3 (1986) 229–272. CrossRef
Rabinowitz, P.H. and Stredulinsky, E., Mixed states for an Allen-Cahn type equation. Commun. Pure Appl. Math. 56 (2003) 1078–1134. CrossRef
Rabinowitz, P.H. and Stredulinsky, E., Mixed states for an Allen-Cahn type equation, II. Calc. Var. Partial Differ. Equ. 21 (2004) 157–207. CrossRef
Rabinowitz, P.H., Heteroclinic for reversible Hamiltonian system. Ergod. Th. Dyn. Sys. 14 (1994) 817–829.
Rabinowitz, P.H., Solutions of heteroclinic type for some classes of semilinear elliptic partial differential equations. J. Math. Sci. Univ. Tokio 1 (1994) 525–550.