Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Bekkers, Erik
Duits, Remco
Berendschot, Tos
and
ter Haar Romeny, Bart
2014.
A Multi-Orientation Analysis Approach to Retinal Vessel Tracking.
Journal of Mathematical Imaging and Vision,
Vol. 49,
Issue. 3,
p.
583.
Bekkers, E. J.
Duits, R.
Mashtakov, A.
and
Sanguinetti, G. R.
2015.
Scale Space and Variational Methods in Computer Vision.
Vol. 9087,
Issue. ,
p.
613.
Bekkers, E. J.
Duits, R.
Mashtakov, A.
and
Sanguinetti, G. R.
2015.
A PDE Approach to Data-Driven Sub-Riemannian Geodesics in $SE$(2).
SIAM Journal on Imaging Sciences,
Vol. 8,
Issue. 4,
p.
2740.
Beschatnyi, I Yu
and
Sachkov, Yu L
2016.
Geodesics in the sub-Riemannian problem on the group SO(3).
Sbornik: Mathematics,
Vol. 207,
Issue. 7,
p.
915.
Beschastnyi, Ivan Yurevich
and
Sachkov, Yurii Leonidovich
2016.
Геодезические в субримановой задаче на группе $\mathrm{SO}(3)$.
Математический сборник,
Vol. 207,
Issue. 7,
p.
29.
Duits, R.
Ghosh, A.
Dela Haije, T. C. J.
and
Mashtakov, A.
2016.
On Sub-Riemannian Geodesics in SE(3) Whose Spatial Projections do not Have Cusps.
Journal of Dynamical and Control Systems,
Vol. 22,
Issue. 4,
p.
771.
Zhang, Jiong
Duits, Remco
Sanguinetti, Gonzalo
and
ter Haar Romeny, Bart M.
2016.
Numerical Approaches for Linear Left-invariant Diffusions onSE(2), their Comparison to Exact Solutions, and their Applications in Retinal Imaging.
Numerical Mathematics: Theory, Methods and Applications,
Vol. 9,
Issue. 1,
p.
1.
Bekkers, Erik J.
Duits, Remco
Mashtakov, Alexey
and
Sachkov, Yuri
2017.
Geometric Science of Information.
Vol. 10589,
Issue. ,
p.
773.
Petitot, Jean
2017.
Elements of Neurogeometry.
p.
347.
Mashtakov, A.
Duits, R.
Sachkov, Yu.
Bekkers, E. J.
and
Beschastnyi, I.
2017.
Tracking of Lines in Spherical Images via Sub-Riemannian Geodesics in $${\text {SO(3)}}$$ SO(3).
Journal of Mathematical Imaging and Vision,
Vol. 58,
Issue. 2,
p.
239.
Boscain, Ugo V.
Chertovskih, Roman
Gauthier, Jean-Paul
Prandi, Dario
and
Remizov, Alexey
2018.
Highly Corrupted Image Inpainting Through Hypoelliptic Diffusion.
Journal of Mathematical Imaging and Vision,
Vol. 60,
Issue. 8,
p.
1231.
Mirebeau, Jean-Marie
2018.
Fast-Marching Methods for Curvature Penalized Shortest Paths.
Journal of Mathematical Imaging and Vision,
Vol. 60,
Issue. 6,
p.
784.
Bekkers, Erik J.
Chen, Da
and
Portegies, Jorg M.
2018.
Nilpotent Approximations of Sub-Riemannian Distances for Fast Perceptual Grouping of Blood Vessels in 2D and 3D.
Journal of Mathematical Imaging and Vision,
Vol. 60,
Issue. 6,
p.
882.
Boscain, U.
Gauthier, J.P.
and
Prandi, D.
2018.
Image inpainting via a control-theoretical model of human vision.
p.
963.
Duits, R.
Meesters, S. P. L.
Mirebeau, J.-M.
and
Portegies, J. M.
2018.
Optimal Paths for Variants of the 2D and 3D Reeds–Shepp Car with Applications in Image Analysis.
Journal of Mathematical Imaging and Vision,
Vol. 60,
Issue. 6,
p.
816.
Chambolle, Antonin
and
Pock, Thomas
2019.
Total roto-translational variation.
Numerische Mathematik,
Vol. 142,
Issue. 3,
p.
611.
Baspinar, E.
Sarti, A.
and
Citti, G.
2020.
A sub-Riemannian model of the visual cortex with frequency and phase.
The Journal of Mathematical Neuroscience,
Vol. 10,
Issue. 1,
Mashtakov, Alexey Pavlovich
2022.
Задача быстродействия на группе движений плоскости с управлением в полукруге.
Математический сборник,
Vol. 213,
Issue. 4,
p.
100.
Bolelli, Maria Virginia
Citti, Giovanna
Sarti, Alessandro
and
Zucker, Steven
2023.
Geometric Science of Information.
Vol. 14071,
Issue. ,
p.
53.
Sachkov, Yurii Leonidovich
2023.
Левоинвариантные задачи оптимального управления на группах Ли, интегрируемые в эллиптических функциях.
Успехи математических наук,
Vol. 78,
Issue. 1(469),
p.
67.
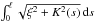 ∫0ℓξ2+K2(s) ds for a planar curve having fixed
initial and final positions and directions. The total length ℓ is free. Here
s is the
arclength parameter, K(s) is the curvature of the curve
and ξ > 0 is a fixed constant. This problem comes from a model of geometry of
vision due to Petitot, Citti and Sarti. We study existence of local and global minimizers
for this problem. We prove that if for a certain choice of boundary conditions there is no
global minimizer, then there is neither a local minimizer nor a geodesic. We finally give
properties of the set of boundary conditions for which there exists a solution to the
problem.
∫0ℓξ2+K2(s) ds for a planar curve having fixed
initial and final positions and directions. The total length ℓ is free. Here
s is the
arclength parameter, K(s) is the curvature of the curve
and ξ > 0 is a fixed constant. This problem comes from a model of geometry of
vision due to Petitot, Citti and Sarti. We study existence of local and global minimizers
for this problem. We prove that if for a certain choice of boundary conditions there is no
global minimizer, then there is neither a local minimizer nor a geodesic. We finally give
properties of the set of boundary conditions for which there exists a solution to the
problem.