Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Beauchard, Karine
2008.
Local Controllability of a One-Dimensional Beam Equation.
SIAM Journal on Control and Optimization,
Vol. 47,
Issue. 3,
p.
1219.
Ervedoza, Sylvain
and
Puel, Jean-Pierre
2009.
Approximate controllability for a system of Schrödinger equations modeling a single trapped ion.
Annales de l'Institut Henri Poincaré C, Analyse non linéaire,
Vol. 26,
Issue. 6,
p.
2111.
Beauchard, Karine
and
Laurent, Camille
2010.
Local controllability of 1D linear and nonlinear Schrödinger equations with bilinear control.
Journal de Mathématiques Pures et Appliquées,
Vol. 94,
Issue. 5,
p.
520.
Beauchard, Karine
2011.
Local controllability and non-controllability for a 1D wave equation with bilinear control.
Journal of Differential Equations,
Vol. 250,
Issue. 4,
p.
2064.
Beauchard, Karine
and
Morancey, Morgan
2014.
Local controllability of 1D Schrödinger equations with bilinear control and minimal time.
Mathematical Control & Related Fields,
Vol. 4,
Issue. 2,
p.
125.
Beauchard, Karine
Lange, Horst
and
Teismann, Holger
2015.
Local Exact Controllability of a One-Dimensional Nonlinear Schrödinger Equation.
SIAM Journal on Control and Optimization,
Vol. 53,
Issue. 5,
p.
2781.
Castelli, Roberto
and
Teismann, Holger
2016.
Rigorous numerics for NLS: Bound states, spectra, and controllability.
Physica D: Nonlinear Phenomena,
Vol. 334,
Issue. ,
p.
158.
Jian Zu
and
Yong Li
2016.
LOCAL EXACT CONTROLLABILITY OF SCHRÖDINGER EQUATION WITH STURM-LIOUVILLE BOUNDARY VALUE PROBLEMS.
Journal of Applied Analysis & Computation,
Vol. 6,
Issue. 3,
p.
851.
Moyano, Iván
2017.
Controllability of a 2D quantum particle in a time-varying disc with radial data.
Journal of Mathematical Analysis and Applications,
Vol. 455,
Issue. 2,
p.
1323.
Chowdhury, Shirshendu
and
Ervedoza, Sylvain
2019.
Open loop stabilization of incompressible Navier–Stokes equations in a 2d channel using power series expansion.
Journal de Mathématiques Pures et Appliquées,
Vol. 130,
Issue. ,
p.
301.
Duca, Alessandro
Joly, Romain
and
Turaev, Dmitry
2020.
Permuting quantum eigenmodes by a quasi-adiabatic motion of a potential wall.
Journal of Mathematical Physics,
Vol. 61,
Issue. 10,
Beauchard, Karine
and
Marbach, Frédéric
2020.
Unexpected quadratic behaviors for the small-time local null controllability of scalar-input parabolic equations.
Journal de Mathématiques Pures et Appliquées,
Vol. 136,
Issue. ,
p.
22.
Duca, Alessandro
and
Joly, Romain
2021.
Schrödinger Equation in Moving Domains.
Annales Henri Poincaré,
Vol. 22,
Issue. 6,
p.
2029.
Li, Lingfei
and
Gao, Hang
2021.
The stability and stabilization of heat equation in non-cylindrical domain.
Journal of Mathematical Analysis and Applications,
Vol. 493,
Issue. 2,
p.
124538.
Bournissou, Mégane
2023.
Quadratic behaviors of the 1D linear Schrödinger equation with bilinear control.
Journal of Differential Equations,
Vol. 351,
Issue. ,
p.
324.
Bournissou, Mégane
2024.
Small-time local controllability of the bilinear Schrödinger equation with a nonlinear competition.
ESAIM: Control, Optimisation and Calculus of Variations,
Vol. 30,
Issue. ,
p.
2.
Balmaseda, Aitor
Lonigro, Davide
and
Pérez-Pardo, Juan Manuel
2024.
On Global Approximate Controllability of a Quantum Particle in a Box by Moving Walls.
SIAM Journal on Control and Optimization,
Vol. 62,
Issue. 2,
p.
826.
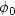 close enough to an eigenstate corresponding to the length l = 1 and $\phi_{f}$
close enough to an eigenstate corresponding to the length l = 1 and $\phi_{f}$ 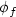 close enough to another eigenstate corresponding to the length l=1, there exists a continuous function $l:[0,T] \rightarrow \mathbb{R}^{*}_{+}$
close enough to another eigenstate corresponding to the length l=1, there exists a continuous function $l:[0,T] \rightarrow \mathbb{R}^{*}_{+}$ 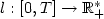 with T > 0, such that l(0) = 1 and l(T) = 1, and which moves the wave function from $\phi_{0}$
with T > 0, such that l(0) = 1 and l(T) = 1, and which moves the wave function from $\phi_{0}$ 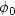 to $\phi_{f}$
to $\phi_{f}$ 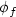 in time T.In particular, we can move the wave function from one eigenstate to another one by acting on the length of the potential well in a suitable way.Our proof relies on local controllability results proved with moment theory, a Nash-Moser implicit function theorem and expansions to the second order.
in time T.In particular, we can move the wave function from one eigenstate to another one by acting on the length of the potential well in a suitable way.Our proof relies on local controllability results proved with moment theory, a Nash-Moser implicit function theorem and expansions to the second order.

