Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Motta, Monica
and
Sartori, Caterina
2007.
Finite Fuel Problem in Nonlinear Singular Stochastic Control.
SIAM Journal on Control and Optimization,
Vol. 46,
Issue. 4,
p.
1180.
Bokanowski, Olivier
Maroso, Stefania
and
Zidani, Hasnaa
2009.
Some Convergence Results for Howard's Algorithm.
SIAM Journal on Numerical Analysis,
Vol. 47,
Issue. 4,
p.
3001.
Aronna, M. Soledad
and
Rampazzo, Franco
2015.
L1limit solutions for control systems.
Journal of Differential Equations,
Vol. 258,
Issue. 3,
p.
954.
Aronna, M.-Soledad
Motta, Monica
and
Rampazzo, Franco
2015.
Infimum Gaps for Limit Solutions.
Set-Valued and Variational Analysis,
Vol. 23,
Issue. 1,
p.
3.
Kunisch, Karl
and
Rao, Zhiping
2017.
Minimal Time Problem with Impulsive Controls.
Applied Mathematics & Optimization,
Vol. 75,
Issue. 1,
p.
75.
Motta, Monica
and
Sartori, Caterina
2018.
Lack of BV bounds for impulsive control systems.
Journal of Mathematical Analysis and Applications,
Vol. 461,
Issue. 1,
p.
422.
El Asri, Brahim
and
Lalioui, Hafid
2023.
Continuous and impulse controls differential game in finite horizon with Nash-equilibrium and application.
Journal of Computational and Applied Mathematics,
Vol. 424,
Issue. ,
p.
115009.
El Asri, Brahim
and
Lalioui, Hafid
2023.
Deterministic differential games in infinite horizon involving continuous and impulse controls.
Journal of Control and Decision,
p.
1.
Daafouz, Jamal
Lohéac, Jérôme
and
Postoyan, Romain
2024.
Mixed Regular and Impulsive Sampled-data LQR.
p.
1625.
Capuzzo Dolcetta, I.
and
Finzi Vita, S.
2024.
At Work with Maurizio: Scattered Notes from a Rich Experience.
Dynamic Games and Applications,
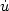 . Adopting a space-time
reparametrization of the problem which adds one variable to the state
space we overcome some difficulties connected to the presence of $\dot u$
. Adopting a space-time
reparametrization of the problem which adds one variable to the state
space we overcome some difficulties connected to the presence of $\dot u$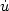 .
We construct an approximation scheme for that augmented system,
prove that it converges to the value function of the augmented
problem and establish an error estimates in L∞ for this
approximation. Moreover, a characterization of the limit of the discrete
optimal controls is given showing that it converges (in a suitable sense)
to an optimal control for the continuous problem.
.
We construct an approximation scheme for that augmented system,
prove that it converges to the value function of the augmented
problem and establish an error estimates in L∞ for this
approximation. Moreover, a characterization of the limit of the discrete
optimal controls is given showing that it converges (in a suitable sense)
to an optimal control for the continuous problem.