Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Schechter, Martin
and
Zou, Wenming
2003.
Weak linking.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 55,
Issue. 6,
p.
695.
Zou, Wenming
2005.
Some recent results in linking theory and applications.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 63,
Issue. 5-7,
p.
e1979.
He, Xiaoming
and
Zou, Wenming
2008.
Nontrivial solitary waves to the generalized Kadomtsev–Petviashvili equations.
Applied Mathematics and Computation,
Vol. 197,
Issue. 2,
p.
858.
Ding, Jian
Xu, Junxiang
Zhang, Fubao
and
Clark, Stephen
2009.
Existence of Homoclinic Orbits for Hamiltonian Systems with Superquadratic Potentials.
Abstract and Applied Analysis,
Vol. 2009,
Issue. 1,
Yang, Minbo
Chen, Wenxiong
and
Ding, Yanheng
2010.
Solutions for periodic Schrödinger equation with spectrum zero and general superlinear nonlinearities.
Journal of Mathematical Analysis and Applications,
Vol. 364,
Issue. 2,
p.
404.
Yang, Minbo
2010.
Nonstationary homoclinic orbits for an infinite-dimensional Hamiltonian system.
Journal of Mathematical Physics,
Vol. 51,
Issue. 10,
Yang, Minbo
Chen, Wenxiong
and
Ding, Yanheng
2010.
Solutions for Discrete Periodic Schrödinger Equations with Spectrum 0.
Acta Applicandae Mathematicae,
Vol. 110,
Issue. 3,
p.
1475.
Yang, Minbo
2010.
Ground state solutions for a periodic Schrödinger equation with superlinear nonlinearities.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 72,
Issue. 5,
p.
2620.
Chen, Guanwei
and
Ma, Shiwang
2011.
Homoclinic orbits of superlinear Hamiltonian systems.
Proceedings of the American Mathematical Society,
Vol. 139,
Issue. 11,
p.
3973.
Chen, Guanwei
and
Ma, Shiwang
2011.
Periodic solutions for Hamiltonian systems without Ambrosetti–Rabinowitz condition and spectrum 0.
Journal of Mathematical Analysis and Applications,
Vol. 379,
Issue. 2,
p.
842.
Schechter, Martin
2012.
Superlinear Schrödinger operators.
Journal of Functional Analysis,
Vol. 262,
Issue. 6,
p.
2677.
Chen, Guanwei
and
Ma, Shiwang
2012.
Discrete nonlinear Schrödinger equations with superlinear nonlinearities.
Applied Mathematics and Computation,
Vol. 218,
Issue. 9,
p.
5496.
Liu, Shibo
2012.
On superlinear Schrödinger equations with periodic potential.
Calculus of Variations and Partial Differential Equations,
Vol. 45,
Issue. 1-2,
p.
1.
Zhang, Jian
Tang, Xianhua
and
Zhang, Wen
2013.
Ground state solutions for nonperiodic Dirac equation with superquadratic nonlinearity.
Journal of Mathematical Physics,
Vol. 54,
Issue. 10,
Chen, GuanWei
and
Ma, ShiWang
2013.
Asymptotically or super linear cooperative elliptic systems in the whole space.
Science China Mathematics,
Vol. 56,
Issue. 6,
p.
1181.
Zhang, Jian
Tang, Xianhua
and
Zhang, Wen
2013.
HOMOCLINIC ORBITS OF NONPERIODIC SUPERQUADRATIC HAMILTONIAN SYSTEM.
Taiwanese Journal of Mathematics,
Vol. 17,
Issue. 6,
Chen, Guanwei
and
Ma, Shiwang
2013.
Ground state periodic solutions of second order Hamiltonian systems without spectrum 0.
Israel Journal of Mathematics,
Vol. 198,
Issue. 1,
p.
111.
Chen, Guanwei
and
Zhao, Xiaoming
2014.
Ground state homoclinic orbits of superquadratic damped vibration systems.
Advances in Difference Equations,
Vol. 2014,
Issue. 1,
Joel Batkam, Cyril
2014.
Homoclinic orbits of first-order superquadratic Hamiltonian systems.
Discrete & Continuous Dynamical Systems - A,
Vol. 34,
Issue. 9,
p.
3353.
Chen, Shaowei
and
Zhang, Dawei
2014.
Existence of Nontrivial Solutions for Periodic Schrödinger Equations with New Nonlinearities.
Abstract and Applied Analysis,
Vol. 2014,
Issue. ,
p.
1.
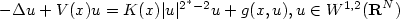 , where N ≥ 4; V,K,g are periodic
in xj for 1 ≤ j ≤ N and 0 is in a gap of the spectrum
of -Δ + V; K>0. If $0<g(x, u)u\leq c|u|^{2^\ast}$
, where N ≥ 4; V,K,g are periodic
in xj for 1 ≤ j ≤ N and 0 is in a gap of the spectrum
of -Δ + V; K>0. If $0<g(x, u)u\leq c|u|^{2^\ast}$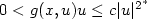 for an
appropriate constant c, we show that this equation has a
nontrivial solution.
for an
appropriate constant c, we show that this equation has a
nontrivial solution.