Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-26T09:13:43.177Z Has data issue: false hasContentIssue false
  • English
  • Français

Uniqueness of renormalized solutions to nonlinear elliptic equations with a lower order term and right-hand side in L 1(Ω)

Published online by Cambridge University Press:  15 August 2002

M. F. Betta ,
A. Mercaldo ,
F. Murat  and
M. M. Porzio
M. F. Betta
Affiliation:
Dipartimento di Matematica, Seconda Università di Napoli, via Vivaldi 43, 81100 Caserta, Italy; [email protected].
A. Mercaldo
Affiliation:
Dipartimento di Matematica e Applicazioni “R. Caccioppoli”, Università degli Studi di Napoli “Federico II", Complesso Monte S. Angelo, via Cintia, 80126 Napoli, Italy; [email protected].
F. Murat
Affiliation:
Laboratoire Jacques-Louis Lions, Université Paris VI, Boîte courrier 187, 75252 Paris Cedex 05, France; [email protected].
M. M. Porzio
Affiliation:
Facoltà di Scienze Matematiche, Fisiche e Naturali, Università degli Studi del Sannio, via Port'Arsa 11, 82100 Benevento, Italy; [email protected].
Get access

Abstract

In this paper we prove uniqueness results for the renormalized solution, if it exists, of a class ofnon coercive nonlinear problems whose prototype is
 $$\left\{- \hbox{div}( a(x)(1+|\nabla u|^{2})^{\frac{p-2}{2}}\nabla u) +b(x)(1+|\nabla u|^{2})^{\frac{\lambda}{2}} =f\hbox{in}\quad\Omega, u=0\hbox{on} \quad \partial\Omega,\right.$$ 
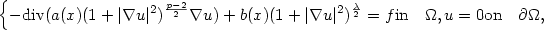where Ω is a bounded open subset of ${\mathbb{R}}^N$ 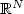, N > 2, 2-1/N < p < N , a belongs to L ∞(Ω), $a(x)\ge\alpha_0>0$ 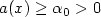,f is a function inL 1(Ω), b is a function in $L^r(\Omega)$ 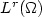and 0 ≤ λ < λ *(N,p,r), for some r and λ *(N,p,r).

Keywords

Uniquenessnonlinear elliptic equationsnoncoercive problemsdata in L 1.
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 8: A tribute to JL Lions , 2002 , pp. 239 - 272
Copyright
© EDP Sciences, SMAI, 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bénilan, P., Boccardo, L., Gallouët, T., Gariepy, R., Pierre, M. and Vazquez, J.L., An L 1-theory of existence and uniqueness of solutions of nonlinear elliptic equations. Ann. Scuola Norm. Sup. Pisa Cl. Sci. 22 (1995) 241-273.
M.F. Betta, A. Mercaldo, F. Murat and M.M. Porzio, Existence and uniqueness results for nonlinear elliptic problems with a lower order term and measure datum. C. R. Acad. Sci. Paris Sér. I Math. 332 (to appear).
M.F. Betta, A. Mercaldo, F. Murat and M.M. Porzio, Existence of renormalized solutions to nonlinear elliptic equations with a lower order term and right-hand side measure. J. Math. Pures Appl. (to appear).
M.F. Betta, A. Mercaldo, F. Murat and M.M. Porzio, Uniqueness results for nonlinear elliptic equations with a lower order term (to appear).
Boccardo, L., Gallouët, T. and Orsina, L., Existence and uniqueness of entropy solutions for nonlinear elliptic equations with measure data. Ann. Inst. H. Poincaré Anal. Non Linéaire 13 (1996) 539-551. CrossRef
Bottaro, G. and Marina, M.E., Problema di Dirichlet per equazioni ellittiche di tipo variazionale su insiemi non limitati. Boll. Un. Mat. Ital. 8 (1973) 46-56.
Dall'Aglio, A., Approximated solutions of equations with L 1 data. Application to the H-convergence of quasi-linear parabolic equations. Ann. Mat. Pura Appl. 170 (1996) 207-240. CrossRef
Dal Maso, G., Murat, F., Orsina, L. and Prignet, A., Renormalized solutions for elliptic equations with general measure data. Ann. Scuola Norm. Sup. Pisa Cl. Sci. 28 (1999) 741-808.
Dolzmann, G., Hungerbühler, N. and Müller, S., Uniqueness and maximal regularity for nonlinear elliptic systems of n-Laplace type with measure valued right-hand side. J. Reine Angew. Math. 520 (2000) 1-35. CrossRef
Fiorenza, A. and Sbordone, C., Existence and uniqueness results for solutions of nonlinear equations with right-hand side in L 1(Ω). Studia Math. 127 (1998) 223-231.
Greco, L., Iwaniec, T. and Sbordone, C., Inverting the p-harmonic operator. Manuscripta Math. 92 (1997) 249-258. CrossRef
Guibé, O., Remarks on the uniqueness of comparable renormalized solutions of elliptic equations with measure data. Ann. Mat. Pura Appl. Ser. IV 180 (2002) 441-449.
P.-L. Lions and F. Murat, Solutions renormalisées d'équations elliptiques non linéaires (to appear).
F. Murat, Soluciones renormalizadas de EDP elipticas no lineales, Preprint 93023. Laboratoire d'Analyse Numérique de l'Université Paris VI (1993).
F. Murat, Équations elliptiques non linéaires avec second membre L 1 ou mesure, in Actes du 26 e Congrès National d'Analyse Numérique. Les Karellis, France (1994) A12-A24.
Prignet, A., Remarks on existence and uniqueness of solutions of elliptic problems with right-hand side measures. Rend. Mat. Appl. 15 (1995) 321-337.
Serrin, J., Pathological solutions of elliptic differential equations. Ann. Scuola Norm. Sup. Pisa Cl. Sci. 18 (1964) 385-387.
Stampacchia, G., Le problème de Dirichlet pour les équations elliptiques du second ordre à coefficients discontinus. Ann. Inst. Fourier (Grenoble) 15 (1965) 189-258. CrossRef