Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-06T16:20:25.339Z Has data issue: false hasContentIssue false
  • English
  • Français

The structure of reachable sets for affine control systemsinduced by generalized Martinet sub-Lorentzian metrics

Published online by Cambridge University Press:  16 January 2012

Marek Grochowski
Marek Grochowski*
Affiliation:
Cardinal Stefan Wyszyński University, Faculty of Mathematics and Natural Sciences Cardinal Stefan Wyszyński, University Dewajtis 5, 01-815 Warszawa, Poland. [email protected] Institute of Mathematics, Polish Academy of Sciences, ul. Śniadeckich 8, 00-950 Warszawa, Poland
Get access

Abstract

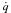In this paper we investigate analytic affine control systems \hbox{$\dot{q}$}q̇ = X + uY, u ∈  [a,b] , whereX,Y is an orthonormal frame for a generalized Martinet sub-Lorentzianstructure of order k of Hamiltonian type. We construct normal forms forsuch systems and, among other things, we study the connection between the presence of thesingular trajectory starting at q0 on the boundary of thereachable set from q0 with the minimal number of analyticfunctions needed for describing the reachable set from q0.

Keywords

Sub-Lorentzian manifoldsgeodesicsreachable setsgeometric optimalityaffine control systems
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 18 , Issue 4 , October 2012 , pp. 1150 - 1177
Copyright
© EDP Sciences, SMAI, 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Références

A. Agrachev and Y. Sachkov, Control Theory from Geometric Viewpoint, Encyclopedia of Mathematical Science 87. Springer (2004).
Agrachev, A., Chakir EL Alaoui, H., and Gauthier, J.P., Sub-Riemannian Metrics on R3, Canadian Mathematical Society Conference Proceedings 25 (1998) 29–78.
A. Bellaïche, The Tangent Space in the sub-Riemannian Geometry, in Sub-Riemannian Geometry. Birkhäuser (1996).
B. Bonnard and M. Chyba, Singular Trajectories and their Role in Control Theory. Springer-Verlag, Berlin (2003).
A. Bressan and B. Piccoli, Introduction to Mathematical Theory of Control. Ameracan Institut of Mathematical Sciences (2007).
Grochowski, M., Normal forms of germes of contact sub-Lorentzian structures on R3. Differentiability of the sub-Lorentzian distance. J. Dyn. Control Syst. 9 (2003) 531–547. Google Scholar
Grochowski, M., Properties of reachable sets in the sub-Lorentzian geometry. J. Geom. Phys. 59 (2009) 885–900. Google Scholar
Grochowski, M., Reachable sets for contact sub-Lorentzian structures on R3. Application to control affine systems on R3 with a scalar input. J. Math. Sci. 177 (2011) 383–394. Google Scholar
Grochowski, M., Normal forms and reachable sets for analytic martinet sub-Lorentzian structures of Hamiltonian type. J. Dyn. Control Syst. 17 (2011) 49–75. Google Scholar
Jakubczyk, B. and Zhitomorskii, M., Singularities and normal forms of generic 2-distributions on 3-manifolds. Stud. Math. 113 (1995) 223–248. Google Scholar
Korolko, A. and Markina, I., Nonholonomic Lorentzian geometry on some H-type groups. J. Geom. Anal. 19 (2009) 864–889. Google Scholar
Liu, W. and Sussmann, H., Shortest paths for sub-Riemannian metrics on Rank-Two distributions. Memoires of the American Mathematical Society 118 (1995) 1–104. Google Scholar
S. Łojasiewicz, Ensembles semi-analytiques. Inst. Hautes Études Sci., Bures-sur-Yvette, France (1964)
M. Zhitomirskii, Typical Singularities of Differential 1-Forms and Pfaffian Equations, Translations of Math. Monographs 113. Amer. Math. Soc. Providence (1991).