Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Neubauer, Andreas
and
Scherzer, Otmar
1998.
Regularization for Curve Representations: Uniform Convergence for Discontinuous Solutions of Ill-Posed Problems.
SIAM Journal on Applied Mathematics,
Vol. 58,
Issue. 6,
p.
1891.
Nashed, M. Z.
and
Scherzer, O.
1998.
Least squares and bounded variation regularization with nondifferentiable functionals.
Numerical Functional Analysis and Optimization,
Vol. 19,
Issue. 7-8,
p.
873.
KÄRKKÄINEN, T.
and
Majava, K.
2000.
Nonmonotone and Monotone Active-Set Methods for Image Restoration, Part 1: Convergence Analysis.
Journal of Optimization Theory and Applications,
Vol. 106,
Issue. 1,
p.
61.
Ring, Wolfgang
2000.
Structural Properties of Solutions to Total Variation Regularization Problems.
ESAIM: Mathematical Modelling and Numerical Analysis,
Vol. 34,
Issue. 4,
p.
799.
Kindermann, Stefan
and
Neubauer, Andreas
2001.
Estimation of discontinuous parameters of elliptic partial differential equations by regularization for surface representations.
Inverse Problems,
Vol. 17,
Issue. 4,
p.
789.
Ngwa, G.
Frigaard, I. A.
and
Scherzer, O.
2003.
On Effective Stopping Time Selection for Visco-Plastic Nonlinear BV Diffusion Filters Used in Image Denoising.
SIAM Journal on Applied Mathematics,
Vol. 63,
Issue. 6,
p.
1911.
Burger, Martin
and
Osher, Stanley
2004.
Convergence rates of convex variational regularization.
Inverse Problems,
Vol. 20,
Issue. 5,
p.
1411.
Chan, Tony F.
and
Tai, Xue-Cheng
2004.
Level set and total variation regularization for elliptic inverse problems with discontinuous coefficients.
Journal of Computational Physics,
Vol. 193,
Issue. 1,
p.
40.
Kunisch, K.
and
Hintermüller, M.
2004.
Total Bounded Variation Regularization as a Bilaterally Constrained Optimization Problem.
SIAM Journal on Applied Mathematics,
Vol. 64,
Issue. 4,
p.
1311.
Osher, Stanley
Burger, Martin
Goldfarb, Donald
Xu, Jinjun
and
Yin, Wotao
2005.
An Iterative Regularization Method for Total Variation-Based Image Restoration.
Multiscale Modeling & Simulation,
Vol. 4,
Issue. 2,
p.
460.
Fu, Haoying
Ng, Michael K.
Nikolova, Mila
and
Barlow, Jesse L.
2006.
Efficient Minimization Methods of Mixed l2-l1 and l1-l1 Norms for Image Restoration.
SIAM Journal on Scientific Computing,
Vol. 27,
Issue. 6,
p.
1881.
Neubauer, A.
2006.
Estimation of discontinuous solutions of ill-posed problems via adaptive grid regularization.
Journal of Inverse and Ill-posed Problems,
Vol. 14,
Issue. 7,
p.
705.
Vasin, V. V.
2006.
Some tendencies in the Tikhonov regularization of ill-posed problems.
Journal of Inverse and Ill-posed Problems,
Vol. 14,
Issue. 8,
p.
813.
Frigaard, I.A.
and
Scherzer, O.
2006.
Herschel-Bulkley diffusion filtering: non-Newtonian fluid mechanics in image processing.
ZAMM,
Vol. 86,
Issue. 6,
p.
474.
Hinterberger, W.
and
Scherzer, O.
2006.
Variational Methods on the Space of Functions of Bounded Hessian for Convexification and Denoising.
Computing,
Vol. 76,
Issue. 1-2,
p.
109.
Vasin, V. V.
and
Korotkii, M. A.
2007.
Tikhonov regularization with nondifferentiable stabilizing functionals.
jiip,
Vol. 15,
Issue. 8,
p.
853.
Hofmann, B
Kaltenbacher, B
Pöschl, C
and
Scherzer, O
2007.
A convergence rates result for Tikhonov regularization in Banach spaces with non-smooth operators.
Inverse Problems,
Vol. 23,
Issue. 3,
p.
987.
Tai, Xue-Cheng
and
Li, Hongwei
2007.
A piecewise constant level set method for elliptic inverse problems.
Applied Numerical Mathematics,
Vol. 57,
Issue. 5-7,
p.
686.
Vasin, V. V.
2007.
Some approaches to reconstruction of nonsmooth solutions of linear ill-posed problems.
jiip,
Vol. 15,
Issue. 6,
p.
625.
Neubauer, Andreas
2007.
Solution of Ill-Posed Problems via Adaptive Grid Regularization: Convergence Analysis.
Numerical Functional Analysis and Optimization,
Vol. 28,
Issue. 3-4,
p.
405.
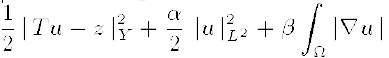 over u ∈ K ∩ X, where α≥ 0, β > 0, K is a closed convex subset of L 2(Ω), and the last additive term denotes the BV-seminorm of u, T is a linear operator from L 2 ∩ BV into the observation space Y. We formulate necessary optimality conditions for (P). Then we show that (P) admits, for givenregularization parameters α and β, solutions which depend in a stable manner on the data z. Finally we study the asymptotic behavior when α = β → 0. The regularized solutions ûβ of (P) converge to the L 2 ∩ BV minimal norm solution of the unregularized problem. The rate of convergence is β½ when the minimum-norm solution û is smooth enough.
over u ∈ K ∩ X, where α≥ 0, β > 0, K is a closed convex subset of L 2(Ω), and the last additive term denotes the BV-seminorm of u, T is a linear operator from L 2 ∩ BV into the observation space Y. We formulate necessary optimality conditions for (P). Then we show that (P) admits, for givenregularization parameters α and β, solutions which depend in a stable manner on the data z. Finally we study the asymptotic behavior when α = β → 0. The regularized solutions ûβ of (P) converge to the L 2 ∩ BV minimal norm solution of the unregularized problem. The rate of convergence is β½ when the minimum-norm solution û is smooth enough.

