Article contents
Oscillations and concentrations generatedby ${\mathcal A}$ 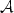 -freemappings and weak lower semicontinuityof integral functionals
-freemappings and weak lower semicontinuityof integral functionals
Published online by Cambridge University Press: 21 April 2009
Abstract
DiPerna's and Majda's generalization of Young measures is used to describe oscillations and concentrations in sequences of maps $\{u_k\}_{k\in{\mathbb N}} \subset L^p(\Omega;{\mathbb R}^m)$ 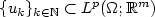 satisfying a linear differential constraint ${\mathcal A}u_k=0$
satisfying a linear differential constraint ${\mathcal A}u_k=0$ 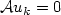 . Applications to sequential weak lower semicontinuity of integral functionals on ${\mathcal A}$
. Applications to sequential weak lower semicontinuity of integral functionals on ${\mathcal A}$ 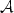 -free sequences and to weak continuity of determinants are given. In particular, we state necessary and sufficient conditions for weak* convergence of det $\nabla\varphi_k\stackrel{*}{\rightharpoonup}{\rm det}\nabla\varphi$
-free sequences and to weak continuity of determinants are given. In particular, we state necessary and sufficient conditions for weak* convergence of det $\nabla\varphi_k\stackrel{*}{\rightharpoonup}{\rm det}\nabla\varphi$ 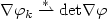 in measures on the closure of $\Omega\subset{\mathbb R}^n$
in measures on the closure of $\Omega\subset{\mathbb R}^n$  if $\varphi_k\rightharpoonup\varphi$
if $\varphi_k\rightharpoonup\varphi$ 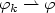 in $W^{1,n}(\Omega;{\mathbb R}^n)$
in $W^{1,n}(\Omega;{\mathbb R}^n)$ 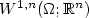 . This convergence holds, for example, under Dirichlet boundary conditions. Further, we formulate a Biting-like lemmaprecisely stating which subsets $\Omega_j\subset \Omega$
. This convergence holds, for example, under Dirichlet boundary conditions. Further, we formulate a Biting-like lemmaprecisely stating which subsets $\Omega_j\subset \Omega$ 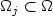 must be removed to obtain weak lower semicontinuity of $u\mapsto\int_{\Omega\setminus\Omega_j} v(u(x))\,{\rm d}x$
must be removed to obtain weak lower semicontinuity of $u\mapsto\int_{\Omega\setminus\Omega_j} v(u(x))\,{\rm d}x$ 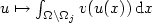 along $\{u_k\}\subset L^p(\Omega;{\mathbb R}^m)\cap{\rm ker}\ {\mathcal A}$
along $\{u_k\}\subset L^p(\Omega;{\mathbb R}^m)\cap{\rm ker}\ {\mathcal A}$ 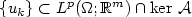 . Specifically, $\Omega_j$
. Specifically, $\Omega_j$ 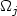 are arbitrarily thin “boundary layers”.
are arbitrarily thin “boundary layers”.
- Type
- Research Article
- Information
- ESAIM: Control, Optimisation and Calculus of Variations , Volume 16 , Issue 2 , April 2010 , pp. 472 - 502
- Copyright
- © EDP Sciences, SMAI, 2009
References
- 15
- Cited by


