Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Champion, Thierry
De Pascale, Luigi
and
Prinari, Francesca
2004.
Γ-convergence and absolute minimizers for supremal functionals.
ESAIM: Control, Optimisation and Calculus of Variations,
Vol. 10,
Issue. 1,
p.
14.
Gori, Michele
and
Maggi, Francesco
2005.
The common root of the geometric conditions in Serrin’s lower semicontinuity theorem.
Annali di Matematica Pura ed Applicata,
Vol. 184,
Issue. 1,
p.
95.
Garroni, Adriana
Ponsiglione, Marcello
and
Prinari, Francesca
2006.
From 1-homogeneous supremal functionals to difference quotients: relaxation and Γ-convergence.
Calculus of Variations and Partial Differential Equations,
Vol. 27,
Issue. 4,
p.
397.
Perego, Mauro
Veneziani, Alessandro
and
Vergara, Christian
2011.
A Variational Approach for Estimating the Compliance of the Cardiovascular Tissue: An Inverse Fluid-Structure Interaction Problem.
SIAM Journal on Scientific Computing,
Vol. 33,
Issue. 3,
p.
1181.
Prinari, Francesca
2015.
On the lower semicontinuity and approximation of $${L^{\infty}}$$ L ∞ -functionals.
Nonlinear Differential Equations and Applications NoDEA,
Vol. 22,
Issue. 6,
p.
1591.
Gelli, Maria Stella
and
Prinari, Francesca
2021.
The role of intrinsic distances in the relaxation of L∞-functionals.
Nonlinear Analysis,
Vol. 204,
Issue. ,
p.
112202.
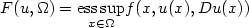 with respect to the strong convergence in L∞(Ω),
furnishing a comparison with the analogous theory developed by
Serrin for integrals. A sort of Mazur's lemma for gradients of uniformly
converging sequences is proved.
with respect to the strong convergence in L∞(Ω),
furnishing a comparison with the analogous theory developed by
Serrin for integrals. A sort of Mazur's lemma for gradients of uniformly
converging sequences is proved.