Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-25T02:25:29.292Z Has data issue: false hasContentIssue false
  • English
  • Français

On a variational problem arising in crystallography

Published online by Cambridge University Press:  14 February 2007

Alexander J. Zaslavski
Alexander J. Zaslavski*
Affiliation:
Department of Mathematics, Technion-Israel Institute of Technology, 32000, Haifa, Israel; [email protected]
Get access

Abstract

We study a variational problem which was introduced by Hannon,Marcus and Mizel [ESAIM: COCV9 (2003) 145–149] todescribe step-terraces on surfaces of so-called “unorthodox” crystals.We show that there is no nondegenerate intervals on which the absolutevalue of a minimizer is $\pi/2$ 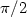identically.

Keywords

Minimizersurfaces of crystalsunorthodox crystalvariational problem.
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 13 , Issue 1 , January 2007 , pp. 72 - 92
Copyright
© EDP Sciences, SMAI, 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Dacorogna, B. and Pfister, C.E., Wulff theorem and best constant in Sobolev inequality. J. Math. Pures Appl. 71 (1992) 97–118.
Fonseca, I., The Wulff theorem revisited. Proc. R. Soc. Lond. A 432 (1991) 125–145. CrossRef
Hannon, J., Bartelt, N.C., Swartzentruber, B.S., Hamilton, J.C. and Kellogg, G.L., Step faceting at the (001) surface of boron doped silicon. Phys. Rev. Lett. 79 (1997) 4226–4229. CrossRef
Hannon, J., Marcus, M. and Mizel, V.J., A variational problem modelling behavior of unorthodox silicon crystals. ESAIM: COCV 9 (2003) 145–149. CrossRef
Jeng, H.C. and Williams, E.D., Steps on surfaces: experiment and theory. Surface Science Reports 34 (1999) 175–294.
Mullins, W.W., Theory of thermal grooving. J. Appl. Physics 28 (1957) 333–339. CrossRef