Published online by Cambridge University Press: 15 February 2004
We compute numerically the minimizers of the Dirichlet energy $$E(u)=\frac{1}{2}\int_{B^2}|\nabla u|^2 {\rm d}x$$ 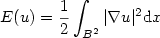 among maps $u:B^2\to S^2$
among maps $u:B^2\to S^2$ 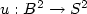 from the unit disc into the unit sphere that satisfy a boundary condition and a degree condition. We use a Sobolev gradient algorithm for the minimization and we prove that its continuous version preserves the degree. For the discretization of the problem we use continuous P 1 finite elements. We propose an original mesh-refining strategy needed to preserve the degree with the discrete version of the algorithm (which is a preconditioned projected gradient). In order to improve the convergence, we generalize to manifolds the classical Newton and conjugate gradient algorithms. We give a proof of the quadratic convergence of the Newton algorithm for manifolds in a general setting.
from the unit disc into the unit sphere that satisfy a boundary condition and a degree condition. We use a Sobolev gradient algorithm for the minimization and we prove that its continuous version preserves the degree. For the discretization of the problem we use continuous P 1 finite elements. We propose an original mesh-refining strategy needed to preserve the degree with the discrete version of the algorithm (which is a preconditioned projected gradient). In order to improve the convergence, we generalize to manifolds the classical Newton and conjugate gradient algorithms. We give a proof of the quadratic convergence of the Newton algorithm for manifolds in a general setting.