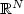Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bögelein, Verena
Duzaar, Frank
Marcellini, Paolo
and
Scheven, Christoph
2018.
Doubly Nonlinear Equations of Porous Medium Type.
Archive for Rational Mechanics and Analysis,
Vol. 229,
Issue. 2,
p.
503.