Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T23:22:48.882Z Has data issue: false hasContentIssue false
  • English
  • Français

Is it wise to keep laminating?

Published online by Cambridge University Press:  15 October 2004

Marc Briane  and
Vincenzo Nesi
Marc Briane
Affiliation:
Centre de Mathématique, INSA de Rennes & IRMAR, 20 avenue des Buttes de Coësmes, 35043 Rennes Cedex, France; [email protected].
Vincenzo Nesi
Affiliation:
Dip. di Mat., Universitá di Roma, La Sapienza P.le A. Moro 2, 00185 Rome, Italy; [email protected].
Get access

Abstract

We study the corrector matrix $P^{\varepsilon}$ 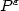 to the conductivity equations. We showthat if $P^{\varepsilon}$  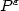converges weakly to the identity, then for any laminate $\det P^{\varepsilon}\geq 0$ 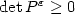at almost every point. This simple property is shown to be false forgeneric microgeometries if the dimension is greater than two in the work Briane et al. [Arch. Ration. Mech. Anal., to appear].In two dimensions it holds true for any microgeometry as a corollary of the work in Alessandrini and Nesi [Arch. Ration. Mech. Anal.158 (2001) 155-171]. We use this property of laminates to prove that, in any dimension, the classicalHashin-Shtrikman bounds are not attained by laminates, in certain regimes, when the number ofphases is greater than two. In addition we establish new bounds for the effective conductivity,which are asymptotically optimal for mixtures of three isotropic phases among a certain class ofmicrogeometries, including orthogonal laminates, which we then call quasiorthogonal.

Keywords

Homogenizationboundscompositeslaminates.
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 10 , Issue 4 , October 2004 , pp. 452 - 477
Copyright
© EDP Sciences, SMAI, 2004

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alessandrini, G. and Nesi, V., Univalent $\sigma$ -harmonic mappings. Arch. Ration. Mech. Anal. 158 (2001) 155-171. CrossRef
Alessandrini, G. and Nesi, V., Univalent $\sigma$ -harmonic mappings: applications to composites. ESAIM: COCV 7 (2002) 379-406. CrossRef
P. Bauman, A. Marini and V. Nesi, Univalent solutions of an elliptic system of partial differential equations arising in homogenization. Indiana Univ. Math. J. 50 (2001) (Spring).
A. Bensoussan, J.L. Lions and G. Papanicolaou, Asymptotic Analysis for Periodic Structures. North-Holland (1978).
Briane, M., Correctors for the homogenization of a laminate. Adv. Math. Sci. Appl. 4 (1994) 357-379.
M. Briane, G.W. Milton and V. Nesi, Change of sign of the corrector's determinant in three dimensions. Arch. Ration. Mech. Anal. To appear.
A. Cherkaev, Variational methods for structural optimization. Appl. Math. Sci. 140 (2000).
Cherkaev, A. and Gibiansky, L.V., Extremal structures of multiphase heat conducting composites. Internat J. Solids Structures 33 (1996) 2609-2618. CrossRef
Gibiansky, L.V. and Sigmund, O., Multiphase composites with extremal bulk modulus. J. Mech. Phys. Solids 48 (2000) 461-498. CrossRef
Hashin, Z. and Shtrikman, S., A variational approach to the theory of effective magnetic permeability of multiphase materials. J. Appl. Phys. 33 (1962) 3125-3131. CrossRef
Lurie, K.A. and Cherkaev, A.V., Exact estimates of conductivity of composites formed by two isotropically conducting media taken in prescribed proportions. Proc. R. Soc. Edinb. A 99 (1984) 71-87. CrossRef
Lurie, K.A. and Cherkaev, A.V., The problem of formation of an optimal isotropic multicomponent composite. J. Opt. Theory Appl. 46 (1985) 571-589. CrossRef
Lurie, K.A. and Cherkaev, A.V., Exact estimates of the conductivity of a binary mixture of isotropic materials. Proc. R. Soc. Edinb. A 104 (1986) 21-38. CrossRef
Milton, G.W., Concerning bounds on transport and mechanical properties of multicomponent composite materials. Appl. Phys A 26 (1981) 125-130. CrossRef
Milton, G.W. and Kohn, R.V., Variational bounds on the effective moduli of anisotropic composites. J. Mech. Phys. Solids 36 (1988) 597-629. CrossRef
Murat, F., Compacité par compensation : condition nécessaire et suffisante de continuité faible sous une hypothèse de rang constant. Ann. Scuola Norm. Sup. Pisa Cl. Sci. 4 (1981) 69-102.
F. Murat, H-convergence. Séminaire d'Analyse Fonctionnelle et Numérique (1977-78), Université d'Alger. English translation: Murat F. and Tartar L., H-convergence. Topics in the Mathematical Modelling of Composite Materials, L. Cherkaev and R.V. Kohn Ed., Birkaüser, Boston, Progr. Nonlinear Differential Equations Appl. (1998) 21-43.
F. Murat and L. Tartar, Calcul des variations et homogénéisation, in Les Méthodes de l'homogénéisation : théorie et applications en physique. Eyrolles (1985) 319-369.
Nesi, V., Using quasiconvex functionals to bound the effective conductivity of composite materials. Proc. R. Soc. Edinb. Sect. A 123 (1993) 633-679. CrossRef
Nesi, V., Bounds on the effective conductivity of $2d$ composites made of $n\geq 3$ isotropic phases in prescribed volume fractions: the weighted translation method. Proc. R. Soc. Edinb. A 125 (1995) 1219-1239. CrossRef
Spagnolo, S., Sul limite delle soluzioni di problemi di Cauchy relativi all'equazione del calore. Ann. Scuola Norm. Sup. Pisa 3 (1967) 657-699.
Spagnolo, S., Sulla convergenza di soluzioni di equazioni paraboliche ed ellittiche. Ann. Scuola Norm. Sup. Pisa 3 (1968) 571-597.
Tartar, L., Estimations de coefficients homogénéisés. Lect. Notes Math. 704 (1978) 364-373
L. Tartar, Estimations fines des coefficients homogénéisés, in Ennio De Giorgi's Colloquium, Paris, 1983, P. Kree Ed., Pitman, Boston (1985) 168-187.
L. Tartar, Compensated compactness and applications to p.d.e. in nonlinear analysis and mechanics, Heriot-Watt Symposium, Vol. IV, R.J. Knops Ed., Pitman, Boston (1979) 136-212.