Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-27T02:40:18.322Z Has data issue: false hasContentIssue false
  • English
  • Français

Infinitely many solutions for asymptotically linear periodicHamiltonian elliptic systems

Published online by Cambridge University Press:  21 October 2008

Fukun Zhao ,
Leiga Zhao  and
Yanheng Ding
Fukun Zhao
Affiliation:
Department of Mathematics, Yunnan Normal University, Kunming 650092 Yunnan, P.R. China. [email protected] Institute of Mathematics, AMSS, CAS, Beijing 100080, P.R. China.
Leiga Zhao
Affiliation:
Department of Mathematics, Beijing University of Chemical technology, Beijing 100029, P.R. China.
Yanheng Ding
Affiliation:
Institute of Mathematics, AMSS, CAS, Beijing 100080, P.R. China.
Get access

Abstract

This paper is concerned with the following periodic Hamiltonianelliptic system

$ \{ -\Delta \varphi+V(x)\varphi=G_\psi(x,\varphi,\psi)\ \hbox{in }\mathbb{R}^N, \\-\Delta \psi+V(x)\psi=G_\varphi(x,\varphi,\psi)\ \hbox{in }\mathbb{R}^N, \\\varphi(x)\to 0\ \hbox{and }\psi(x)\to0\ \hbox{as }|x|\to\infty.$

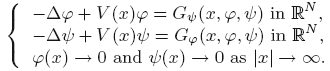
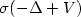Assuming the potential V is periodic and 0 lies in a gap of $\sigma(-\Delta+V)$ , $G(x,\eta)$ 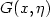is periodic in x andasymptotically quadratic in $\eta=(\varphi,\psi)$ 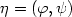, existence andmultiplicity of solutions areobtained via variational approach.


Keywords

Hamiltonian elliptic systemvariational methodsstrongly indefinite functionals
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 16 , Issue 1 , January 2010 , pp. 77 - 91
Copyright
© EDP Sciences, SMAI, 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ackermann, N., On a periodic Schrödinger equation with nonlinear superlinear part. Math. Z. 248 (2004) 423–443. CrossRef
Ackermann, N., A superposition principle and multibump solutions of periodic Schrödinger equations. J. Func. Anal. 234 (2006) 277–320. CrossRef
Alves, C.O., Carrião, P.C. and Miyagaki, O.H., On the existence of positive solutions of a perturbed Hamiltonian system in $\mathbb{R}^N$ . J. Math. Anal. Appl. 276 (2002) 673–690. CrossRef
Ávila, A.I. and Yang, J., On the existence and shape of least energy solutions for some elliptic systems. J. Diff. Eq. 191 (2003) 348–376. CrossRef
Ávila, A.I. and Yang, J., Multiple solutions of nonlinear elliptic systems. Nonlinear Differ. Equ. Appl. 12 (2005) 459–479. CrossRef
T. Bartsch and D.G. De Figueiredo, Infinitely many solutions of nonlinear elliptic systems, in Progress in Nonlinear Differential Equations and Their Applications 35, Birkhäuser, Basel/Switzerland (1999) 51–67.
Bartsch, T. and Ding, Y., Deformation theorems on non-metrizable vector spaces and applications to critical point theory. Math. Nach. 279 (2006) 1–22. CrossRef
Benci, V. and Rabinowitz, P.H., Critical point theorems for indefinite functionals. Inven. Math. 52 (1979) 241–273. CrossRef
Coti-Zelati, V. and Rabinowitz, P.H., Homoclinic orbits for second order Hamiltonian systems possessing superquadratic potentials. J. Amer. Math. Soc. 4 (1991) 693–727. CrossRef
Coti-Zelati, V. and Rabinowitz, P.H., Homoclinic type solutions for a semilinear elliptic PDE on $\mathbb{R}^N$ . Comm. Pure Appl. Math. 45 (1992) 1217–1269.
De Figueiredo, D.G. and Ding, Y.H., Strongly indefinite functionals and multiple solutions of elliptic systems. Trans. Amer. Math. Soc. 355 (2003) 2973–2989. CrossRef
De Figueiredo, D.G. and Felmer, P.L., On superquadratic elliptic systems. Trans. Amer. Math. Soc. 343 (1994) 97–116. CrossRef
De Figueiredo, D.G. and Yang, J., Decay, symmetry and existence of solutions of semilinear elliptic systems. Nonlinear Anal. 33 (1998) 211–234. CrossRef
De Figueiredo, D.G., Marcos, J. do Ó and B. Ruf, An Orlicz-space approach to superlinear elliptic systems. J. Func. Anal. 224 (2005) 471–496. CrossRef
Ding, Y. and Jeanjean, L., Homoclinic orbits for a non periodic Hamiltonian system. J. Diff. Eq. 237 (2007) 473–490. CrossRef
Ding, Y. and Lin, F.H., Semiclassical states of Hamiltonian systems of Schrödinger equations with subcritical and critical nonlinearies. J. Partial Diff. Eqs. 19 (2006) 232–255.
Hulshof, J. and Van de Vorst, R.C.A.M., Differential systems with strongly variational structure. J. Func. Anal. 114 (1993) 32–58. CrossRef
Kryszewski, W. and Szulkin, A., An infinite dimensional Morse theory with applications. Trans. Amer. Math. Soc. 349 (1997) 3181–3234. CrossRef
Kryszewski, W. and Szulkin, A., Generalized linking theorem with an application to semilinear Schrödinger equations. Adv. Differential Equations 3 (1998) 441–472.
Li, G. and Szulkin, A., An asymptotically periodic Schrödinger equation with indefinite linear part. Comm. Contemp. Math. 4 (2002) 763–776. CrossRef
Li, G. and Yang, J., Asymptotically linear elliptic systems. Comm. Partial Diff. Eq. 29 (2004) 925–954. CrossRef
Pistoia, A. and Ramos, M., Locating the peaks of the least energy solutions to an elliptic system with Neumann boundary conditions. J. Diff. Eq. 201 (2004) 160–176. CrossRef
M. Reed and B. Simon, Methods of Modern Mathematical Physics, IV Analysis of Operators. Academic Press, New York (1978).
Séré, E., Existence of infinitely many homoclinic orbits in Hamiltonian stysems. Math. Z. 209 (1992) 133–160. CrossRef
Sirakov, B., On the existence of solutions of Hamiltonian elliptic systems in RN . Adv. Differential Equations 5 (2000) 1445–1464.
Troestler, C. and Willem, M., Nontrivial solution of a semilinear Schrödinger equation. Comm. Partial Diff. Eq. 21 (1996) 1431–1449. CrossRef
M. Willem, Minimax Theorems. Birkhäuser, Berlin (1996).
Yang, J., Nontrivial solutions of semilinear elliptic systems in $\mathbb{R}^N$ . Electron. J. Diff. Eqns. 6 (2001) 343–357.