Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Buttazzo, G.
Carlier, G.
and
Tahraoui, R.
2010.
On Some Systems Controlled by the Structure of Their Memory.
SIAM Journal on Control and Optimization,
Vol. 48,
Issue. 8,
p.
5241.
Zhou, Jianjun
2019.
Delay optimal control and viscosity solutions to associated Hamilton–Jacobi–Bellman equations.
International Journal of Control,
Vol. 92,
Issue. 10,
p.
2263.
Kim, Yeoneung
Tran, Hung V.
and
Tu, Son N.
2020.
State-Constraint Static Hamilton--Jacobi Equations in Nested Domains.
SIAM Journal on Mathematical Analysis,
Vol. 52,
Issue. 5,
p.
4161.
Lemos-Paião, Ana P.
Silva, Cristiana J.
and
Torres, Delfim F. M.
2020.
Mathematical Modelling and Analysis of Infectious Diseases.
Vol. 302,
Issue. ,
p.
323.
de Feo, Filippo
2024.
Stochastic optimal control problems with delays in the state and in the control via viscosity solutions and applications to optimal advertising and optimal investment problems.
Decisions in Economics and Finance,
Gomoyunov, Mikhail Igorevich
and
Lukoyanov, Nikolai Yur'evich
2024.
Минимаксные решения уравнений Гамильтона-Якоби в задачах динамической оптимизации наследственных систем.
Успехи математических наук,
Vol. 79,
Issue. 2(476),
p.
43.
Zhou, Jianjun
2024.
Viscosity solutions to second order elliptic Hamilton-Jacobi–Bellman equations with infinite delay.
The Annals of Applied Probability,
Vol. 34,
Issue. 5,
Gomoyunov, Mikhail Igorevich
and
Lukoyanov, Nikolai Yur'evich
2024.
Minimax solutions of Hamilton-Jacobi equations in dynamic optimization problems for hereditary systems.
Russian Mathematical Surveys,
Vol. 79,
Issue. 2,
p.
229.
De Feo, Filippo
Federico, Salvatore
and
Święch, Andrzej
2024.
Optimal Control of Stochastic Delay Differential Equations and Applications to Path-Dependent Financial and Economic Models.
SIAM Journal on Control and Optimization,
Vol. 62,
Issue. 3,
p.
1490.
de Feo, Filippo
and
Święch, Andrzej
2025.
Optimal control of stochastic delay differential equations: Optimal feedback controls.
Journal of Differential Equations,
Vol. 420,
Issue. ,
p.
450.
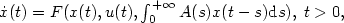
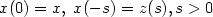 .
.  the solution of the previous Cauchy problem and:
the solution of the previous Cauchy problem and: