Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-06T04:00:31.291Z Has data issue: false hasContentIssue false
  • English
  • Français

Eliciting harmonics on strings

Published online by Cambridge University Press:  18 January 2008

Steven J. Cox  and
Antoine Henrot
Steven J. Cox
Affiliation:
Computational and Applied Mathematics, Rice University, Houston, TX, USA; [email protected]
Antoine Henrot
Affiliation:
Institut Élie Cartan, UMR 7502, Nancy Université - CNRS - INRIA, Nancy, France.
Get access

Abstract

One may produce the qth harmonic of a string of length π by applying the 'correct touch' at the node $\pi/q$ 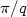during a simultaneous pluck or bow. This notion wasmade precise by a model of Bamberger, Rauch and Taylor. Their 'touch' isa damper of magnitude b concentrated at $\pi/q$ 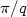. The 'correct touch' is that b for which the modes, that do not vanishat $\pi/q$ 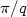, are maximally damped. We here examine the associated spectralproblem. We find the spectrum to be periodic and determined by a polynomialof degree $q-1$ . We establish lower and upper bounds on the spectral abscissaand show that the set of associated root vectors constitutes a Riesz basisand so identify 'correct touch' with the b that minimizes the spectral abscissa.

Keywords

Point-wise dampingspectral abscissaRiesz basis
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 14 , Issue 4 , October 2008 , pp. 657 - 677
Copyright
© EDP Sciences, SMAI, 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ammari, K., Henrot, A. and Tucsnak, M., Asymptotic behavior of the solutions and optimal location of the actuator for the pointwise stabilization of a string. Asymptot. Anal. 28 (2001) 215–240.
Bamberger, A., Rauch, J. and Taylor, M., A model for harmonics on stringed instruments. Arch. Rational Mech. Anal. 79 (1982) 267–290. CrossRef
G. Banat, Masters of the Violin, Sonatas for the Violin, Jean-Joseph Cassanéa de Mondonville 5. Johnson Reprint (1982).
Bernoulli, D., Réflexions et éclaircissemens sur les nouvelles vibrations des cordes exposées dans les mémoires de 1747 and 1748. Histoire de l'Academie royale des sciences et belles lettres 9 (1753) 148–172.
A.S. Birch and M.A. Srinivasan, Experimental determination of the viscoelastic properties of the human fingerpad. Touch Lab Report 14, RLE TR-632, MIT, Cambridge (1999).
J.T. Cannon and S. Dostrovsky, The Evolution of Dynamics, Vibration Theory from 1687 to 1742. Springer, New York (1981).
T. Christensen, Rameau and Musical Thought in the Enlightenment. Cambridge (1993).
S.J. Cox, Aye there's the rub, An inquiry into how a damped string comes to rest, in Six Themes on Variation, R. Hardt Ed., AMS (2004) 37–58.
Cox, S. and Zuazua, E., The rate at which energy decays in a damped string. Comm. Partial Diff. Eq. 19 (1994) 213–243. CrossRef
Cox, S. and Zuazua, E., The rate at which energy decays in a string damped at one end. Indiana U. Math. J. 44 (1995) 545–573. CrossRef
Cuzzucoli, G. and Lombardo, V., A physical model of the classical guitar, including the player's touch. Comput. Music J. 23 (1999) 52–69. CrossRef
Galpin, F.W., Monsieur Prin and his trumpet marine. Music Lett. 14 (1933) 18–29. CrossRef
C. Girdlestone, Jean-Philippe Rameau. Cassell, London (1957).
Guo, B.-Z. and Xie, Y., A sufficient condition on Riesz basis with parenthesis of nonself-adjoint operator and application to a serially connected string system under joint feedbacks. SIAM J. Control Optim. 43 (2004) 1234–1252. CrossRef
H. Helmholtz, On the Sensations of Tone. Dover (1954).
Jaffard, S., Tucsnak, M. and Zuazua, E., Singular internal stabilization of the wave equation. J. Diff. Eq. 145 (1998) 184–215. CrossRef
Kergomard, J., Debut, V. and Matignon, D., Resonance modes in a 1-D medium with two purely resistive boundaries: calculation methdos, orthogogonality and completeness. J. Acoust. Soc. Am. 119 (2006) 1356–1367. CrossRef
Kovács, I., Zur Frage der Seilschwingungen und der Seildämpfung. Die Bautechnik 59 (1982) 325–332.
Krein, M.G. and Langer, H., On some mathematical principles in the linear theory of damped oscillations of continua I. Integr. Equ. Oper. Theory 1 (1978) 364–399. CrossRef
Krein, M.G. and Nudelman, A.A., On direct and inverse problems for the boundary dissipation frequencies of a nonuniform string. Soviet Math. Dokl. 20 (1979) 838–841.
Krenk, S., Vibrations of a taut cable with an external damper. J. Appl. Mech. 67 (2000) 772–776. CrossRef
Liu, K.S., Energy decay problems in the design of a pointwise stabilizer for string vibrating systems. SIAM J. Control Optim. 26 (1988) 1248–1256. CrossRef
M. Marden, Geometry of Polynomials. AMS (1966).
D.C. Miller, Anecdotal History of the Science of Sound. Macmillan, New York (1935).
J.-P. Rameau, Generation Harmonique, Facsimile of 1737 Paris Ed., Broude Brothers, New York (1966).
J.W.S. Rayleigh, Theory of Sound, Vol. 1. Dover (1945).
Roberts, F., A discourse concerning the musical notes of the trumpet, and trumpet-marine, and of the defects of the same. Philosophical Transactions 16 (1692) 559–563. CrossRef
J. Sauveur, Systéme général des intervalles des sons et son application à tous les systémes et à tous les instrumens de musique, Mémoires de l'Académie royale des sciences 1701. Amsterdam (1707) 390–482.
Taylor, B., Moti Nervi Tensi, De. Philosophical Transactions 28 (1713) 26–32. CrossRef
C. Truesdell, The Rational Mechanics of Flexible or Elastic Bodies, 1638–1788, introduction to Leonhardi Euleri Opera Omnia Vols. 10 and 11, Series 2, Leipzig (1912).
J. Tyndall, Sound. D. Appleton (1875).
Wallis, J., Concerning a new musical discovery. Philosophical Transactions 12 (1677) 839–842. CrossRef
Xu, G.-Q. and Guo, B.-Z., Riesz basis property of evolution equations in Hilbert spaces and application to a coupled string equation. SIAM J. Control Optim. 42 (2003) 966–984. CrossRef
R.M. Young, An Introduction to Nonharmonic Fourier Series. Academic Press, San Diego (2001).
T. Young, A Course of Lectures on Natural Philosophy and the Mechanical Arts. Johnson Reprint (1971).
Zukovsky, P., On violin harmonics. Perspectives of New Music 6 (1968) 174–181. CrossRef