Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T11:06:39.009Z Has data issue: false hasContentIssue false
  • English
  • Français

Curl bounds Grad on SO(3)

Published online by Cambridge University Press:  21 September 2007

Patrizio Neff  and
Ingo Münch
Patrizio Neff
Affiliation:
Department of Mathematics, Technische Universität Darmstadt, Schlossgartenstrasse 7, 64289 Darmstadt, Germany; [email protected]
Ingo Münch
Affiliation:
Institut für Baustatik, Universität Karlsruhe (TH), Kaiserstrasse 12, 76131 Karlsruhe, Germany; [email protected]
Get access

Abstract

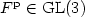Let $F^{\rm p} \in {\rm GL}(3)$ be the plastic deformation from the multiplicative decomposition in elasto-plasticity. We show that the geometric dislocation density tensor of Gurtin in the form ${\rm Curl}[{F^{\rm p}}]\cdot (F^{\rm p})^T$ 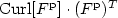applied to rotations controls the gradient in the sense that pointwise $ \forall R \in C^1(\mathbb{R}^3, {\rm SO}(3)): \Arrowvert {\rm Curl}[R] \cdot R^T \Arrowvert_{\mathbb{M}^{3\times3}}^2 \ge \frac{1}{2} \Arrowvert{\rm D}R\Arrowvert_{\mathbb{R}^{27}}^2$ 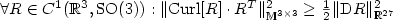.This result complements rigidity results[Friesecke, James and Müller, Comme Pure Appl. Math.55 (2002) 1461–1506; John, Comme Pure Appl. Math.14 (1961) 391–413; Reshetnyak, Siberian Math. J.8 (1967) 631–653)] as well as an associated linearized theorem saying that $ \forall A \in C^1(\mathbb{R}^3, \mathfrak{so}(3)): \Arrowvert {\rm Curl}[A]\Arrowvert_{\mathbb{M}^{3\times3}}^2 \ge \frac{1}{2} \Arrowvert{\rm D}A\Arrowvert_{\mathbb{R}^{27}}^2 = \Arrowvert\nabla{\rm axl}[A]\Arrowvert_{\mathbb{R}^9}^2$ .

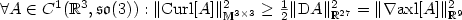Keywords

Rotationspolar-materialsmicrostructuredislocation densityrigiditydifferential geometrystructured continua
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 14 , Issue 1 , January 2008 , pp. 148 - 159
Copyright
© EDP Sciences, SMAI, 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

S. Aubry and M. Ortiz, The mechanics of deformation-induced subgrain-dislocation structures in metallic crystals at large strains. Proc. R. Soc. Lond., Ser. A, Math. Phys. Eng. Sci. 459 (2003) 3131–3158.
B.A. Bilby, R. Bullough and E. Smith, Continuous distributions of dislocations: a new application of the methods of non-riemannian geometry. Proc. Roy. Soc. London, Ser. A 231 (1955) 263–273.
E. Cartan, Leçons sur la géometrie des espaces de Riemann. Gauthier-Villars, Paris (1928).
Cermelli, P. and Gurtin, M.E., On the characterization of geometrically necessary dislocations in finite plasticity. J. Mech. Phys. Solids 49 (2001) 1539–1568. CrossRef
Conti, S. and Ortiz, M., Dislocation microstructures and the effective behavior of single crystals. Arch. Rat. Mech. Anal. 176 (2005) 103–147. CrossRef
A. Einstein, Relativity: The Special and General Theory. Crown, New-York (1961).
J.D. Eshelby, The continuum theory of lattice defects, volume III of Solid state Physics. Academic Press, New-York (1956).
Friesecke, G., James, R.D. and Müller, S., A theorem on geometric rigidity and the derivation of nonlinear plate theory from three-dimensional elasticity. Comm. Pure Appl. Math. 55 (2002) 1461–1506. CrossRef
M.E. Gurtin, An Introduction to Continuum Mechanics, Mathematics in Science and Engineering 158. Academic Press, London, 1st edn. (1981).
Gurtin, M.E., On the plasticity of single crystals: free energy, microforces, plastic-strain gradients. J. Mech. Phys. Solids 48 (2000) 989–1036. CrossRef
J.P. Hirth and J. Lothe, Theory of Dislocations. McGraw-Hill, New-York (1968).
John, F., Rotation and strain. Comm. Pure Appl. Math. 14 (1961) 391–413. CrossRef
J. Jost, Riemannian Geometry. Springer-Verlag (2002).
K. Kondo, Geometry of elastic deformation and incompatibility, in Memoirs of the Unifying Study of the Basic Problems in Engineering Science by Means of Geometry, volume 1, Division C, K. Kondo Ed., Gakujutsu Bunken Fukyo-Kai (1955) 361–373.
Kröner, E., Der fundamentale Zusammenhang zwischen Versetzungsdichte und Spannungsfunktion. Z. Phys. 142 (1955) 463–475. CrossRef
E. Kröner, Kontinuumstheorie der Versetzungen und Eigenspannungen, Ergebnisse der Angewandten Mathematik 5. Springer, Berlin (1958).
Kröner, E., Allgemeine Kontinuumstheorie der Versetzungen und Eigenspannungen. Arch. Rat. Mech. Anal. 4 (1960) 273–334. CrossRef
Kröner, E. and Seeger, A., Nichtlineare Elastizitätstheorie der Versetzungen und Eigenspannungen. Arch. Rat. Mech. Anal. 3 (1959) 97–119. CrossRef
Kuhlmann-Wilsdorf, D., Theory of plastic deformation: properties of low energy dislocation structures. Mat. Sci. Eng. A113 (1989) 1. CrossRef
Lee, E.H., Elastic-plastic deformation at finite strain. J. Appl. Mech. 36 (1969) 1–6. CrossRef
Mielke, A. and Müller, S., Lower semi-continuity and existence of minimizers in incremental finite-strain elastoplasticity. ZAMM 86 (2006) 233–250. CrossRef
T. Mura, Micromechanics of defects in solids. Kluwer Academic Publishers, Boston (1987).
F.R.N. Nabarro, Theory of crystal dislocations. Oxford University Press, Oxford (1967).
J. Necas and I. Hlavacek, Mathematical theory of elastic and elastico-plastic bodies: An introduction. Elsevier, Amsterdam (1981).
Neff, P., Korn's, On first inequality with nonconstant coefficients. Proc. Roy. Soc. Edinb. A 132 (2002) 221–243. CrossRef
Nye, J.F., Some geometrical relations in dislocated crystals. Acta Metall. 1 (1953) 153–162. CrossRef
Ortiz, M. and Repetto, E.A., Nonconvex energy minimization and dislocation structures in ductile single crystals. J. Mech. Phys. Solids 47 (1999) 397–462. CrossRef
Ortiz, M., Repetto, E.A. and Stainier, L., A theory of subgrain dislocation structures. J. Mech. Phys. Solids 48 (2000) 2077–2114. CrossRef
G.P. Parry and M. Silhavy, Elastic scalar invariants in the theory of defective crystals. R. Soc. Lond. Proc., Ser. A, Math. Phys. Eng. Sci. 455 (1999) 4333–4346.
Reshetnyak, Yu.G., Liouville's theorem on conformal mappings for minimal regularity assumptions. Siberian Math. J. 8 (1967) 631–653. CrossRef
Svendsen, B., Continuum thermodynamic models for crystal plasticity including the effects of geometrically necessary dislocations. J. Mech. Phys. Solids 50 (2002) 1297–1329. CrossRef
R.M. Wald, General Relativity. University of Chicago Press, Chicago (1984).