Published online by Cambridge University Press: 20 July 2007
We study the asymptotic behaviour of a sequence of stronglydegenerate parabolic equations $\partial_t (r_h u) - {\rm div}(a_h \cdot Du)$ 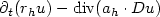 with $r_h(x,t) \geq0$
with $r_h(x,t) \geq0$ 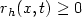 , $r_h \in L^{\infty}(\Omega\times (0,T))$
, $r_h \in L^{\infty}(\Omega\times (0,T))$ 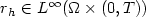 .The main problem is the lack of compactness, by-passed via a regularity result.As particular cases, we obtain G-convergence for elliptic operators $(r_h \equiv 0)$
.The main problem is the lack of compactness, by-passed via a regularity result.As particular cases, we obtain G-convergence for elliptic operators $(r_h \equiv 0)$ 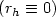 ,G-convergence for parabolic operators $(r_h \equiv 1)$
,G-convergence for parabolic operators $(r_h \equiv 1)$ 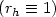 , singular perturbationsof an elliptic operator $(a_h \equiv a$
, singular perturbationsof an elliptic operator $(a_h \equiv a$ 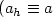 and $r_h \to r$
and $r_h \to r$  , possibly $r\equiv 0)$
, possibly $r\equiv 0)$ 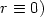 .
.