Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-24T02:37:06.704Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic behavior of nonlinear systemsin varying domains with boundary conditions on varying sets

Published online by Cambridge University Press:  23 January 2009

Carmen Calvo-Jurado ,
Juan Casado-Díaz  and
Manuel Luna-Laynez
Carmen Calvo-Jurado
Affiliation:
Dpto. de Matemáticas, Escuela Politécnica, Avenida de la Universidad s/n, 10071 Cáceres, Spain. [email protected]
Juan Casado-Díaz
Affiliation:
Dpto. de Ecuaciones Diferenciales y Análisis Numérico, Fac. de Matemáticas, C. Tarfia s/n, 41012 Sevilla, Spain. [email protected]; [email protected]
Manuel Luna-Laynez
Affiliation:
Dpto. de Ecuaciones Diferenciales y Análisis Numérico, Fac. de Matemáticas, C. Tarfia s/n, 41012 Sevilla, Spain. [email protected]; [email protected]
Get access

Abstract


For a fixed bounded open set $\Omega\subset\mathbb{R}^N$ 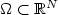, a sequence of open sets $\Omega_n\subset\Omega$ 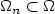and a sequence of sets $\Gamma_n\subset\partial\Omega\cap\partial\Omega_n$ 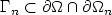, we study theasymptotic behavior of the solution of a nonlinear ellipticsystem posed on $\Omega_n$ 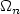, satisfying Neumann boundary conditionson $\Gamma_n$ 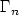and Dirichlet boundary conditions on  $\partial\Omega_n\setminus \Gamma_n$ 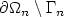. We obtain a representationof the limit problem which is stable by homogenization and weprove that this representation depends on $\Omega_n$ 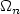and $\Gamma_n$ 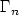locally.


Keywords

Homogenizationvaryingdomainsnonlinear problems
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 15 , Issue 1 , January 2009 , pp. 49 - 67
Copyright
© EDP Sciences, SMAI, 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Calvo-Jurado, C. and Casado-Díaz, J., The limit of Dirichlet systems for variable monotone operators in general perforated domains. J. Math. Pures Appl. 81 (2002) 471–493. CrossRef
Calvo-Jurado, C., Casado-Díaz, J. and Luna-Laynez, M., Homogenization of elliptic problems with the Dirichlet and Neumann conditions imposed on varying subsets. Math. Meth. Appl. Sci. 30 (2007) 1611–1625. CrossRef
Casado-Díaz, J., Homogenization of general quasi-linear Dirichlet problems with quadratic growth in perforated domains. J. Math. Pures Appl. 76 (1997) 431–476. CrossRef
Casado-Díaz, J., Homogenization of Dirichlet problems for monotone operators in varying domains. Proc. Roy. Soc. Edinburgh A 127 (1997) 457–478. CrossRef
Casado-Díaz, J. and Garroni, A., Asymptotic behavior of nonlinear elliptic systems on varying domains. SIAM J. Math. Anal. 31 (2000) 581–624. CrossRef
D. Cionarescu and F. Murat, Un terme étrange venu d'ailleurs, in Nonlinear partial differential equations and their applications, Collège de France seminar, Vols. II and III, H. Brézis and J.-L. Lions Eds., Research Notes in Math. 60 and 70, Pitman, London (1982) 98–138 and 154–78.
Dal Maso, G. and Defranceschi, A., Limits of nonlinear Dirichlet problems in varying domains. Manuscripta Math. 61 (1988) 251–278. CrossRef
Dal Maso, G. and Garroni, A., New results on the asymptotic behaviour of Dirichlet problems in perforated domains. Math. Mod. Meth. Appl. Sci. 3 (1994) 373–407. CrossRef
Dal Maso, G. and Mosco, U., Wiener-criterion and $\Gamma$ -convergence. Appl. Math. Optim. 15 (1987) 15–63. CrossRef
Dal Maso, G. and Murat, F., Asymptotic behaviour and correctors for the Dirichlet problems in perforated domains with homogeneous monotone operators. Ann. Sc. Norm. Sup. Pisa 7 (1997) 765–803.
Dal Maso, G. and Murat, F., Asymptotic behaviour and correctors for linear Dirichlet problems with simultaneously varying operators and domains. Ann. Inst. H. Poincaré Anal. Non Linéaire 21 (2004) 445–486. CrossRef
Dal Maso, G., Garroni, A. and Skrypnik, I.V., A capacitary method for the asymptotic analysis of Dirichlet problems for monotone operators. J. Anal. Math. 71 (1997) 263–313. CrossRef
Damlamian, A. and Boundary, T. Li homogenization for elliptic problems. J. Math. Pures Appl. 66 (1987) 351–361.
L.C. Evans and R.F. Gariepy, Measure Theory and Fine Properties of Functions. CRC Press, Boca Raton (1992).
Federer, H. and Ziemer, W.P., The Lebesgue set of a function whose distribution derivaties are p-th power sumable. Indiana Univ. Math. J. 22 (1972) 139–158. CrossRef
Leray, J. and Lions, J.-L., Quelques résultats de Visik sur les problèmes elliptiques non linéaires par les méthodes de Minty-Browder. Bull. Soc. Math. France 93 (1965) 97–107. CrossRef
J. Necas, Les méthodes directes en théorie des équations elliptiques. Masson, Paris (1967).
Serrin, J., Local behaviour of solutions of quasilinear equations. Acta Math. 111 (1964) 302–347. CrossRef
Skrypnik, I.V., Asymptotic behaviour of solutions of nonlinear elliptic problems in perforated domains. Mat. Sb. 184 (1993) 67–90.
Skrypnik, I.V., Averaging of quasilinear parabolic problems in domains with fine-grained boundary. Diff. Equations 31 (1995) 327–339.
W.P. Ziemer, Weakly Differentiable Functions. Springer-Verlag, Berlin (1989).