In the 1950's and 1960's surface physicists/metallurgists such as Herring and Mullins applied ingenious thermodynamic arguments to explain a number of experimentally observed surface phenomena in crystals. These insights permitted the successful engineering of a large number of alloys, where the major mathematical novelty was that the surface response to external stress was anisotropic. By examining step/terrace (vicinal) surface defects it was discovered through lengthy and tedious experiments that the stored energy density (surface tension) along a step edge was a smooth symmetric function β of the azimuthal angle θ to the step, and that the positive function β attains its minimum value at $\theta = \pi/2$ 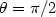and its maximum value at $\theta = 0$ . The function β provided the crucial thermodynamic parameters needed for the engineering of these materials. Moreover the minimal energy configuration of the step is determined by the values of the stiffness function $\beta'' + \beta$ 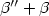which ultimately leads to the magnitude and direction of surface mass flow for these materials. In the 1990's there was a dramatic improvement in electron microscopy which permitted real time observation of the meanderings of a step edge under Brownian heat oscillations. These observations provided much more rapid determination of the relevant thermodynamic parameters for the step edge, even for crystals at temperatures below their roughening temperature. Use of these tools led J. Hannon and his coexperimenters to discover that some crystals behave in a highly anti-intuitive manner as their temperature is varied. The present article is devoted to a model described by a class of variational problems. The main result of the paper describes the solutions of the corresponding problem for a generic integrand.