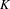 $K$-theory
$K$-theoryPublished online by Cambridge University Press: 02 May 2017
We study irreducible Smale spaces with totally disconnected stable sets and their associated 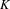 $K$-theoretic invariants. Such Smale spaces arise as Wieler solenoids, and we restrict to those arising from open surjections. The paper follows three converging tracks: one dynamical, one operator algebraic and one
$K$-theoretic invariants. Such Smale spaces arise as Wieler solenoids, and we restrict to those arising from open surjections. The paper follows three converging tracks: one dynamical, one operator algebraic and one 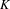 $K$-theoretic. Using Wieler’s theorem, we characterize the unstable set of a finite set of periodic points as a locally trivial fibre bundle with discrete fibres over a compact space. This characterization gives us the tools to analyse an explicit groupoid Morita equivalence between the groupoids of Deaconu–Renault and Putnam–Spielberg, extending results of Thomsen. The Deaconu–Renault groupoid and the explicit Morita equivalence lead to a Cuntz–Pimsner model for the stable Ruelle algebra. The
$K$-theoretic. Using Wieler’s theorem, we characterize the unstable set of a finite set of periodic points as a locally trivial fibre bundle with discrete fibres over a compact space. This characterization gives us the tools to analyse an explicit groupoid Morita equivalence between the groupoids of Deaconu–Renault and Putnam–Spielberg, extending results of Thomsen. The Deaconu–Renault groupoid and the explicit Morita equivalence lead to a Cuntz–Pimsner model for the stable Ruelle algebra. The 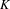 $K$-theoretic invariants of Cuntz–Pimsner algebras are then studied using the Cuntz–Pimsner extension, for which we construct an unbounded representative. To elucidate the power of these constructions, we characterize the Kubo–Martin–Schwinger (KMS) weights on the stable Ruelle algebra of a Wieler solenoid. We conclude with several examples of Wieler solenoids, their associated algebras and spectral triples.
$K$-theoretic invariants of Cuntz–Pimsner algebras are then studied using the Cuntz–Pimsner extension, for which we construct an unbounded representative. To elucidate the power of these constructions, we characterize the Kubo–Martin–Schwinger (KMS) weights on the stable Ruelle algebra of a Wieler solenoid. We conclude with several examples of Wieler solenoids, their associated algebras and spectral triples.