Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T01:04:06.576Z Has data issue: false hasContentIssue false
  • English
  • Français

Whirly 3-interval exchange transformations

Published online by Cambridge University Press:  20 October 2015

YUE WU
YUE WU*
Affiliation:
3519 Heartland Key LN, Katy, TX 77494, USA email [email protected] Schlumberger PTS Full Waveform Inversion Center of Excellence, Houston, TX, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

Irreducible interval exchange transformations are studied with regard to the whirly property, a condition for a non-trivial spatial factor. A uniformly whirly transformation is defined and is further studied. An equivalent condition is introduced for the whirly transformation. We will prove that almost all 3-interval exchange transformations are whirly, using a combinatorics approach with application of the Rauzy–Veech induction. It is still an open question whether the whirly property is a generic property for $m$-interval exchange transformations for 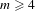$m\geq 4$.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 3 , May 2017 , pp. 995 - 1008
Copyright
© Cambridge University Press, 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Avila, A. and Forni, G.. Weak mixing for interval exchange transformations and translation flows. Ann. of Math. (2) 165(2) (2007), 637–664.Google Scholar
Boshernitzan, M.. A condition for minimal interval exchange maps to be uniquely ergodic. Duke Math. J. 52(3) (1985), 723–752.Google Scholar
Chacon, R. V.. Weakly mixing transformations which are not strongly mixing. Proc. Amer. Math. Soc. 22 (1969), 559–562.Google Scholar
Chaika, J.. Every transformation is disjoint from almost every IET. Ann. of Math. (2) 175 (2012), 237–253.Google Scholar
Chaika, J. and Fickenscher, J.. Topological mixing for some residual sets of interval exchange transformations. Comm. Math. Phys. 333 (2014), 483–503.Google Scholar
Glasner, E.. Ergodic Theory via Joinings (Mathematical Surveys and Monographs, 101) . American Mathematical Society, Providence, RI, 2003.CrossRefGoogle Scholar
Glasner, E., Tsirelson, B. and Weiss, B.. The automorphism group of the Gaussian measure cannot act pointwisely. Israel J. Math. 148(1) (2005), 305–329.Google Scholar
Glasner, E. and Weiss, B.. G-continuous functions and whirly actions. Preprint, 2003, arXiv:math.DS/0311450.Google Scholar
Glasner, E. and Weiss, B.. Spatial and non-spatial actions of Polish groups. Ergod. Th. & Dynam. Sys. 25(5) (2005), 1521–1538.Google Scholar
Halmos, P. R.. Measure Theory (Graduate Texts in Mathematics, 18) . Springer, Berlin, 1976.Google Scholar
Halmos, P. R.. Lectures on Ergodic Theory. Chelsea Publishing Company, New York, 1956.Google Scholar
Keane, M.. Interval exchange transformations. Math Z. 141 (1973), 25–31.Google Scholar
King, J. L.. The commutant is the weak closure of the powers, for rank-1 transformations. Ergod. Th. & Dynam. Sys. 6(3) (1986), 363–384.CrossRefGoogle Scholar
Masur, H.. Interval exchange transformation and measured foliation. Ann. of Math. (2) 115 (1982), 169–200.CrossRefGoogle Scholar
Rauzy, G.. Echanges d’intervalles et transformations induites. Acta Arith. 34 (1979), 315–328.Google Scholar
Veech, W. A.. Interval exchange transformations. J. Anal. Math. 33 (1978), 222–278.CrossRefGoogle Scholar
Veech, W. A.. Projective Swiss cheeses and unique ergodic interval exchange transformations. Ergodic Theory and Dynamical Systems (Progress in Mathematics, I) . Birkhäuser, Boston, MA, 1981, pp. 113–193.Google Scholar
Veech, W. A.. Gauss measures for transformations on the space of interval exchange maps. Ann. of Math. (2) 115 (1982), 201–242.Google Scholar
Veech, W. A.. The metric theory of interval exchange transformations I: generic spectral properties. Amer. J. Math. 107(6) (1984), 1331–1359.Google Scholar
Viana, M.. Ergodic theory of interval exchange maps. Rev. Mat. Complut. 19(1) (2006), 7–100.Google Scholar
Wu, Y.. Applications of Rauzy induction on the generic ergodic theory of interval exchange transformations. PhD Thesis, Rice University Electronic Theses and Dissertations, 2006.Google Scholar