Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T00:28:43.337Z Has data issue: false hasContentIssue false
  • English
  • Français

Viscous stability of quasi-periodic tori

Published online by Cambridge University Press:  27 November 2012

ZHENGUO LIANG ,
JUN YAN  and
YINGFEI YI
ZHENGUO LIANG
Affiliation:
School of Mathematical Sciences and Key Lab of Mathematics for Nonlinear Science, Fudan University, Shanghai 200433, China (email: [email protected], [email protected])
JUN YAN
Affiliation:
School of Mathematical Sciences and Key Lab of Mathematics for Nonlinear Science, Fudan University, Shanghai 200433, China (email: [email protected], [email protected])
YINGFEI YI
Affiliation:
School of Mathematics, Georgia Institute of Technology, Atlanta, GA 30332, USA College of Mathematics, Jilin University, Changchun 130012, PR China (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper is devoted to the study of 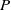$P$-regularity of viscosity solutions 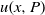$u(x,P)$, 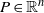$P\in {\Bbb R}^n$, of a smooth Tonelli Lagrangian 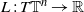$L:T {\Bbb T}^n \rightarrow {\Bbb R}$ characterized by the cell equation 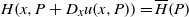$H(x,P+D_xu(x,P))=\overline {H}(P)$, where 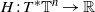$H: T^* {\Bbb T}^n\rightarrow {\Bbb R}$ denotes the Hamiltonian associated with 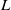$L$ and 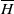$\overline {H}$ is the effective Hamiltonian. We show that if 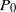$P_0$ corresponds to a quasi-periodic invariant torus with a non-resonant frequency, then 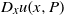$D_xu(x,P)$ is uniformly Hölder continuous in 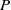$P$ at 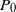$P_0$ with Hölder exponent arbitrarily close to 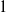$1$, and if both 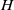$H$ and the torus are real analytic and the frequency vector of the torus is Diophantine, then 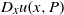$D_xu(x,P)$ is uniformly Lipschitz continuous in 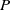$P$ at 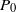$P_0$, i.e., there is a constant 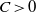$C\gt 0$ such that 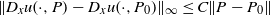$\|D_xu(\cdot ,P)-D_xu(\cdot ,P_0)\|_{\infty }\le C\|P-P_0\|$ for 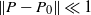$\|P-P_0\|\ll 1$. Similar P-regularity of the Peierls barriers associated with 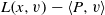$L(x,v)- \langle P,v \rangle $is also obtained.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 34 , Issue 1 , February 2014 , pp. 185 - 210
Copyright
Copyright © 2012 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Arnold, V. I.. Instability of dynamical systems with several degrees of freedom. Sov. Math. Doklady 5 (1964), 581–585.Google Scholar
[2]Bernard, P.. The dynamics of pseudographs in convex Hamiltonian systems. J. Amer. Math. Soc. 21 (2008), 615–669.Google Scholar
[3]Bernard, P.. Symplectic aspects of Mather theory. Duke Math. J. 136 (2007), 401–420.Google Scholar
[4]Bernard, P.. The action spectrum near positive definite invariant tori. Bull. Soc. Math. France 131 (2003), 603–616.CrossRefGoogle Scholar
[5]Bessi, U.. An approach to Arnold’s diffusion through the calculus of variations. Nonlinear Anal. 26 (1996), 1115–1135.Google Scholar
[6]Cheng, C.-Q. and Yan, J.. Existence of diffusion orbits in a priori unstable Hamiltonian systems. J. Differential Geom. 67 (2004), 457–517.Google Scholar
[7]Cheng, C.-Q. and Yan, J.. Arnold diffusion in Hamiltonian systems: the a priori unstable case. J. Differential Geom. 82 (2009), 229–277.CrossRefGoogle Scholar
[8]Chow, S.-N., Li, Y. and Yi, Y.. Persistence of invariant tori on sub-manifolds in Hamiltonian systems. J. Nonlinear Sci. 12 (2002), 585–617.CrossRefGoogle Scholar
[9]Contreras, G., Iturriaga, R., Paternain, G. P. and Paternain, M.. Lagrangian graphs, minimizing measures and Mañé’s crtical values. Geom. Funct. Anal. 8 (1998), 788–809.Google Scholar
[10]Delshams, A., de la Llave, R. and Seara, T.. A geometric mechanism for diffusion in Hamiltonian systems overcoming the large gap problem: announcement of results. Electron. Res. Announc. Amer. Math. Soc. 9 (2003), 125–134.Google Scholar
[11]Evans, L. C. and Gariepy, R. F.. Measure Theory and Fine Properties of Functions (Studies in Advanced Mathematics). CRC Press, Boca Raton, FL, 1992.Google Scholar
[12]Evans, L. C. and Gomes, D.. Effective Hamiltonians and averaging for Hamiltonian dynamics I. Arch. Ration. Mech. Anal. 157 (2001), 1–33.Google Scholar
[13]Fathi, A.. Weak KAM Theorem in Lagrangian Dynamics. Seventh Preliminary Version 2006. Cambridge University Press, Cambridge.Google Scholar
[14]Fathi, A., Giuliani, A. and Sorrentino, A.. Uniqueness of invariant Lagrangian graphs in a homology or a cohomology class. Ann. Sc. Norm. Super. Pisa Cl. Sci. 4 (2009), 659–680.Google Scholar
[15]Gomes, D.. Perturbation theory for viscosity solutions of Hamilton–Jacobi equations and stability of Aubry–Mather sets. SIAM J. Math. Anal. 35 (2003), 135–147.Google Scholar
[16]Gomes, D.. Regularity theory for Hamilton–Jacobi equations. J. Differential Equations 187 (2003), 359–374.Google Scholar
[17]Herman, M.. Sur les courbes invariantes par les difféomorphismes de l’anneau I. Astérisque 103–104 (1983).Google Scholar
[18]Iturriaga, R.. Minimizing measures for time-dependent Lagrangians. Proc. Lond. Math. Soc. 73 (1996), 216–240.Google Scholar
[19]Kaloshin, V. and Levi, M.. An example of Arnold diffusion for near-integrable Hamiltonians. Bull. Amer. Math. Soc. (N.S.) 45 (2008), 409–427.Google Scholar
[20]Kaloshin, V. and Levi, M.. Geometry of Arnold diffusion. SIAM Rev. 50 (2008), 702–720.Google Scholar
[21]Liang, Z. and Yan, J.. Strong stability of KAM tori: from the point of view of viscosity solutions of H–J equations. J. Dynam. Differential Equations 21 (2009), 353–370.Google Scholar
[22]Liang, Z. and Yan, J.. Regularity of viscosity solutions near KAM torus. Sci. China 51 (2008), 361–368.Google Scholar
[23]Lions, P. L., Papanicolaou, G. and Varadhan, S. R. S.. Homogeneization of Hamilton–Jacobi equations. Preprint, 1987, unpublished.Google Scholar
[24]Lochak, P.. Canonical perturbation theory via simultaneous approximation. Uspekhi Mat. Nauk. 47 (1992), 59–140.Google Scholar
[25]Mather, J. N.. Modulus of Continuity for Peierls’s Barrier (Periodic Solutions of Hamiltonian Systems and Related Topics) (NATO ASI Series, 209). Eds. Rabinowitz, P. H.et al. D. Reidel, Dordrecht, 1987, pp. 177–202.Google Scholar
[26]Mather, J. N.. Action minimizing invariant measures for positive Lagrangian systems. Math. Z. 207 (1991), 169–207.Google Scholar
[27]Mather, J. N.. Variational construction of connecting orbits. Ann. Inst. Fourier (Grenoble) 43 (1993), 1349–1386.Google Scholar
[28]Mather, J. N.. Arnold diffusion I: announcement of results. J. Math. Sci. 124 (2004), 5275–5289.Google Scholar
[29]Mather, J. N.. Total disconnectedness of the quotient Aubry set in low dimensions. Comm. Pure Appl. Math. 56 (2003), 1178–1183.Google Scholar
[30]Morbidelli, A. and Giorgilli, A.. Superexponential stability of KAM tori. J. Stat. Phys. 78 (1995), 1607–1617.Google Scholar
[31]Pöschel, J.. A lecture on the classical KAM theorem. Proc. Symp. Pure Math. 69 (2001), 707–732.Google Scholar
[32]Salamon, D. and Zehnder, E.. KAM theory in configuration space. Comment. Math. Helv. 64 (1989), 84–132.Google Scholar
[33]Siburg, K. F.. Aubry–Mather theory and the inverse spectral problem for planar convex domains. Israel J. Math. 113 (1999), 285–304.Google Scholar
[34]Siburg, K. F.. Symplectic invariants of elliptic fixed points. Comment. Math. Helv. 75 (2000), 681–700.Google Scholar
[35]Siburg, K. F.. The Principle of Least Action in Geometry and Dynamics (Lecture Notes in Mathematics, 1844). Springer, Berlin, 2004.Google Scholar
[36]Treschev, D.. Evolution of slow variables in a priori unstable Hamiltonian systems. Nonlinearity 17 (2004), 1803–1841.Google Scholar
[37]Xia, Z.. Arnold diffusion: a variational construction. Proc. Int. Congr. Math., Vol. II (Berlin, 1998), Extra Vol. II, 867–877 (1998) (electronic).Google Scholar
[38]Xia, Z.. Arnold diffusion and instabilities in Hamiltonian dynamics. Preprint.Google Scholar