Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-29T10:45:36.275Z Has data issue: false hasContentIssue false
  • English
  • Français

Variational construction of positive entropy invariant measures of Lagrangian systems and Arnold diffusion

Published online by Cambridge University Press:  25 September 2018

SINIŠA SLIJEPČEVIĆ
SINIŠA SLIJEPČEVIĆ*
Affiliation:
Department of Mathematics, Bijenička 30, University of Zagreb, Croatia email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We develop a variational method for constructing positive entropy invariant measures of Lagrangian systems without assuming transversal intersections of stable and unstable manifolds, and without restrictions to the size of non-integrable perturbations. We apply it to a family of 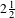$2\frac{1}{2}$ degrees of freedom a priori unstable Lagrangians, and show that if we assume that there is no topological obstruction to diffusion (precisely formulated in terms of topological non-degeneracy of minima of the Peierls barrier), then there exists a vast family of ‘horseshoes’, such as ‘shadowing’ ergodic positive entropy measures having precisely any closed set of invariant tori in its support. Furthermore, we give bounds on the topological entropy and the ‘drift acceleration’ in any part of a region of instability in terms of a certain extremal value of the Fréchet derivative of the action functional, generalizing the angle of splitting of separatrices. The method of construction is new, and relies on study of formally gradient dynamics of the action (coupled parabolic semilinear partial differential equations on unbounded domains). We apply recently developed techniques of precise control of the local evolution of energy (in this case the Lagrangian action), energy dissipation and flux.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 3 , March 2020 , pp. 799 - 864
Copyright
© Cambridge University Press, 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Angenent, S.. A variational interpretation of Mel’nikov’s function and exponentially small separatrix splitting. Symplectic Geometry (London Mathematical Society Lecture Note Series, 192) . Cambridge University Press, Cambridge, 1993, pp. 5–35.Google Scholar
Arnold, V. I.. Instability of dynamical systems with several degrees of freedom. Soviet. Math. Dokl. 5 (1964), 581–585.Google Scholar
Avila, A., Crovisier, S. and Wilkinson, A.. Diffeomorphisms with positive metric entropy. Publ. Math. Inst. Hautes Études Sci. 124 (2016), 319–347.Google Scholar
Bernard, P.. Perturbation d’un hamiltonien partiellement hyperbolique. C. R. Acad. Sci. Paris Sér. I 323 (1996), 189–134.Google Scholar
Bernard, P.. The dynamics of pseudographs in convex Hamiltonian systems. J. Amer. Math. Soc. 21 (2008), 615–669.Google Scholar
Bernard, P.. Arnold diffusion: from the a priori unstable to the a priori stable case. Proceedings of the International Congress of Mathematicians (Hyderabad, India, 2010). Vol. 3. Hindustan Book Agency, New Dehli, 2010, pp. 1680–1700.Google Scholar
Bernard, P., Kaloshin, V. and Zhang, K.. Arnold diffusion in arbitrary degrees of freedom and normally hyperbolic invariant cylinders. Acta Math. 217(1) (2016), 1–79.Google Scholar
Berti, M., Biasco, L. and Bolle, P.. Drift in phase space: a new variational mechanism with optimal diffusion time. J. Math. Pures Appl. (9) 82 (2003), 613–664.Google Scholar
Berti, M. and Bolle, P.. A functional analysis approach to Arnold diffusion. Ann. Inst. H. Poncaré Anal. Non Linéaire 19 (2002), 395–450.Google Scholar
Berti, M. and Bolle, P.. Fast Arnold diffusion in systems with three time scales. Discrete Contin. Dyn. Syst. 8 (2002), 795–811.Google Scholar
Bessi, U.. An approach to Arnold diffusion through the calculus of variations. Nonlinear Anal. 26 (1996), 1115–1135.Google Scholar
Cheng, C.. Variational construction of diffusion ofbits for positive definite Lagrangians. Proceedings of the International Congress of Mathematicians (Hyderabad, India, 2010). Vol. 3. Hindustan Book Agency, New Dehli, 2010, pp. 1714–1728.Google Scholar
Cheng, C. and Yan, J.. Existence of diffusion orbits in a-priori unstable Hamiltonian systems. J. Differential Geom. 67 (2004), 457–517.Google Scholar
Cheng, C. and Yan, J.. Arnold diffusion in Hamiltonian systems: a priori unstable case. J. Differential Geom. 82 (2009), 229–277.Google Scholar
Cherchia, L and Gallavotti, G.. Drift and diffusion in phase space. Ann. Inst. H. Poincaré Phys. Théor. 60 (1994), 144 pp.Google Scholar
Evans, L. C.. Partial Differential Equations, 2nd edn. American Mathematical Society, Providence, RI, 2010.Google Scholar
Fathi, A. Weak KAM Theorem in Lagrangian Dynamics, book preprint, 5th edn.Google Scholar
Gallay, T. and Slijepčević, S.. Energy flow in formally gradient partial differential equations on unbounded domains. J. Dynam. Differential Equations 13 (2001), 757–789. Zbl 1003.35085, MR 1860285.Google Scholar
Gallay, T. and Slijepčević, S.. Energy bounds for the two-dimensional Navier–Stokes equations in an infinite cylinder. Comm. Partial Differential Equations 39 (2014), 1741–1769.Google Scholar
Gallay, T. and Slijepčević, S.. Distribution of energy and convergence to equilibria in extended dissipative systems. J. Dynam. Differential Equations 27 (2015), 653–682.Google Scholar
Gallay, T. and Slijepčević, S.. Uniform boundedness and long-time asymptotics for the two-dimensional Navier–Stokes equations in an infinite cylinder. J. Math. Fluid Mech. 17 (2015), 23–46.Google Scholar
Gelfreich, V. and Turaev, D.. Arnold diffusion in a priory chaotic Hamiltonian systems. Preprint, 2014, arXiv:1406.2945.Google Scholar
Henry, D.. Geometric Theory of Semilinear Parabolic Equations (Lecture Notes in Mathematics, 840) . Springer, Berlin, 1981.Google Scholar
Kaloshin, V. and Zhang, K.. Arnold diffusion for smooth convex systems of two and a half degrees of freedom. Nonlinearity 28 (2015), 2699–2720.Google Scholar
Knill, O.. The problem of positive Kologorov–Sinai entropy for the standard map. Preprint, 1999, arXiv:math/9908014v2.Google Scholar
de la Llave, R.. Some recent progress in geometric methods in the instability problem in Hamiltonian mechanics. Proceedings of the International Congress of Mathematicians (Zürich, 2006). Vol. 2. European Mathematical Society, Zurich, 2006, pp. 1705–1729.Google Scholar
Lochak, P.. Arnold diffusion; a compendium of remarks and questions. Hamiltonian Systems with Three or More Degrees of Freedom (NATO Adv. Sci. Inst. Ser. C Math. Phys. Sci., 533) . Kluwer, Dordrecht, 1999, pp. 168–183.Google Scholar
MacKay, R. S., Meiss, J. D. and Percival, I. C.. Transport in Hamiltoonian systems. Phys. D 13 (1983), 55–81.Google Scholar
Mather, J.. More Denjoy minimal sets for area preserving diffeomorphisms. Comment. Math. Helv. 60 (1985), 508–557.Google Scholar
Mather, J.. Action minimizing measures for positive definite Lagrangian systems. Math. Z. 207 (1991), 169–207.Google Scholar
Mather, J.. Variational construction of connecting orbits. Ann. Inst. Fourier (Grenoble) 43 (1993), 1349–1386.Google Scholar
Mather, J.. Arnold diffusion by variational mathods. Essays in Mathematics and its Applications. Springer, Heidelberg, 2012, pp. 271–285.Google Scholar
Nekhoroshev, N.. An exponential estimate of the time of stability of Hamiltonian systems close to integrable. Uspekhi Mat. Nauk. 32 (1977), 5–66 (in Russian); Engl. Trans. Russian Math. Surveys 32 (1977), 1–65.Google Scholar
Pohožaev, S. I.. The set of critical values of functionals. Mat. Sb. (N.S.) 75 (1968), 106–111.Google Scholar
Simo, C. and Valls, C.. A formal approximation of the splitting of separatrices in the classical Arnold’s example of diffusion with two equal parameters. Nonlinearity 14 (2001), 1707–1760.Google Scholar
Slijepčević, S.. Monotone gradient dynamics and Mather’s shadowing. Nonlinearity 12 (1999), 969–986.Google Scholar
Slijepčević, S.. Extended gradient systems: dimension one. Discrete Contin. Dyn. Syst. (2000), 503–518. Zbl 1009.37004, MR 1757384.Google Scholar
Slijepčević, S.. A new measure of instability and topological entropy of area-preserving twist diffeomorphisms. Rad Hrvat. Akad. Znan. Umjet. Mat. Znan. 21 (2017), 117–141.Google Scholar
Sorrentino, A.. Lecture Notes on Mather’s Theory for Lagrangian Systems. Publ. Mat. Urug. 16 (2016), 169–192.Google Scholar
Treschev, D.. Evolution of slow variables in a-priori unstable Hamiltonian systems. Nonlinearity 17 (2004), 1803–1841.Google Scholar
Treschev, D.. Arnold diffusion far from strong resonances in multidimensional a priori unstable Hamiltonian systems. Nonlinearity 25 (2012), 2717–2757.Google Scholar
Walters, P.. An Introduction to Ergodic Theory. Springer, Heidelberg, 2000.Google Scholar
Zhang, K.. Speed of Arnold diffusion for analytic Hamiltonian systems. Invent. Math. 186 (2011), 255–290.Google Scholar