Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T19:48:12.535Z Has data issue: false hasContentIssue false
  • English
  • Français

Uniformly perfect finitely generated simple left orderable groups

Part of: Abstract harmonic analysis Special aspects of infinite or finite groups

Published online by Cambridge University Press:  08 October 2019

JAMES HYDE ,
YASH LODHA ,
ANDRÉS NAVAS  and
CRISTÓBAL RIVAS
JAMES HYDE
Affiliation:
Mathematical Institute, University of St. Andrews, UK email [email protected]
YASH LODHA
Affiliation:
Institute of Mathematics, École Polytechnique Fédérale de Lausanne, Lausanne, Switzerland email [email protected]
ANDRÉS NAVAS
Affiliation:
Departamento de Matemáticas y Ciencia de la Computación, Universidad de Santiago de Chile, Santiago, Chile Unidad Cuernavaca Instituto de Matemáticas, Universidad Nacional Autónoma de México, Cuernavaca, Mexico email [email protected]
CRISTÓBAL RIVAS
Affiliation:
Departamento de Matemáticas y Ciencia de la Computación, Universidad de Santiago de Chile, Mexico email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that the finitely generated simple left orderable groups $G_{\!\unicode[STIX]{x1D70C}}$ constructed by the first two authors in Hyde and Lodha [Finitely generated infinite simple groups of homeomorphisms of the real line. Invent. Math. (2019), doi:10.1007/s00222-019-00880-7] are uniformly perfect—each element in the group can be expressed as a product of three commutators of elements in the group. This implies that the group does not admit any homogeneous quasimorphism. Moreover, any non-trivial action of the group on the circle, which lifts to an action on the real line, admits a global fixed point. It follows that any faithful action on the real line without a global fixed point is globally contracting. This answers Question 4 of the third author [A. Navas. Group actions on 1-manifolds: a list of very concrete open questions. Proceedings of the International Congress of Mathematicians, Vol. 2. Eds. B. Sirakov, P. Ney de Souza and M. Viana. World Scientific, Singapore, 2018, pp, 2029–2056], which asks whether such a group exists. This question has also been answered simultaneously and independently, using completely different methods, by Matte Bon and Triestino [Groups of piecewise linear homeomorphisms of flows. Preprint, 2018, arXiv:1811.12256]. To prove our results, we provide a characterization of elements of the group 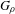$G_{\!\unicode[STIX]{x1D70C}}$ which is a useful new tool in the study of these examples.

Keywords

groups of homeomorphismsorderable groupssimple groups

MSC classification

Primary: 43A07: Means on groups, semigroups, etc.; amenable groups
Secondary: 20F05: Generators, relations, and presentations
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 2 , February 2021 , pp. 534 - 552
Check for updates
Copyright
© Cambridge University Press, 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Altinel, T. and Muranov, A.. Interpretation of the arithmetic in certain groups of piecewise affine permutations of an interval. J. Inst. Math. Jussieu 8(4) (2009), 623–652.CrossRefGoogle Scholar
Belk, J.. Thompson’s group $F$ . Preprint, 2004, arXiv:0708.3609.Google Scholar
Burger, M. and Monod, N.. Continuous bounded cohomology and applications to rigidity theory. Geom. Funct. Anal. 12(2) (2002), 219–280.CrossRefGoogle Scholar
Calegari, D.. scl (MSJ Memoirs, 20) . Mathematical Society of Japan, Tokyo, 2009.CrossRefGoogle Scholar
Cannon, J. W., Floyd, W. J. and Parry, W. R.. Introductory notes on Richard Thompson’s groups. Enseign. Math. 42(3–4) (1996), 215–256.Google Scholar
Deroin, B., Navas, A. and Rivas, C.. Groups, orders, and dynamics. Preprint, arXiv:1408.5805 (version 2016).Google Scholar
Ghys, É.. Groupes d’homéomorphismes du cercle et cohomologie bornée. The Lefschetz Centennial Conference, Part III (Mexico City, 1984) (Contemp. Math., 58, III) . American Mathematical Society, Providence, RI, 1987, pp. 81–106.CrossRefGoogle Scholar
Ghys, É.. Actions de réseaux sur le cercle. Invent. Math. 137(1) (1999), 199–231.CrossRefGoogle Scholar
Hyde, J. and Lodha, Y.. Finitely generated infinite simple groups of homeomorphisms of the real line. Invent. Math. (2019), doi:10.1007/s00222-019-00880-7.CrossRefGoogle Scholar
Lifschitz, L. and Morris Witte, D.. Bounded generation and lattices that cannot act on the line. Pure Appl. Math. Q. 4(1) (2008), 99–126.CrossRefGoogle Scholar
Lifschitz, L. and Morris Witte, D.. Isotropic nonarchimedean S-arithmetic groups are not left orderable. C. R. Math. Acad. Sci. Paris 339(6) (2004), 417–420.CrossRefGoogle Scholar
Matte Bon, N. and Triestino, M.. Groups of piecewise linear homeomorphisms of flows. Preprint, 2018, arXiv:1811.12256.Google Scholar
Navas, A.. Group actions on 1-manifolds: a list of very concrete open questions. Proceedings of the International Congress of Mathematicians, Vol. 2. Eds. Sirakov, B., Ney de Souza, P. and Viana, M.. World Scientific, Singapore, 2018, pp. 2029–2056.Google Scholar
Witte, D.. Arithmetic groups of higher Q-rank cannot act on 1-manifolds. Proc. Amer. Math. Soc. 122(2) (1994), 333–340.Google Scholar