No CrossRef data available.
Published online by Cambridge University Press: 15 February 2023
Let 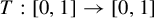 $ T:[0,1]\to [0,1] $ be an expanding Markov map with a finite partition. Let
$ T:[0,1]\to [0,1] $ be an expanding Markov map with a finite partition. Let 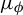 $ \mu _\phi $ be the invariant Gibbs measure associated with a Hölder continuous potential
$ \mu _\phi $ be the invariant Gibbs measure associated with a Hölder continuous potential 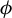 $ \phi $. For
$ \phi $. For 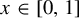 $ x\in [0,1] $ and
$ x\in [0,1] $ and 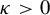 $ \kappa>0 $, we investigate the size of the uniform approximation set
$ \kappa>0 $, we investigate the size of the uniform approximation set  $$ \begin{align*}\mathcal U^\kappa(x):=\{y\in[0,1]:\text{ for all } N\gg1, \text{ there exists } n\le N, \text{ such that }|T^nx-y|<N^{-\kappa}\}.\end{align*} $$
$$ \begin{align*}\mathcal U^\kappa(x):=\{y\in[0,1]:\text{ for all } N\gg1, \text{ there exists } n\le N, \text{ such that }|T^nx-y|<N^{-\kappa}\}.\end{align*} $$
The critical value of 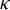 $ \kappa $ such that
$ \kappa $ such that 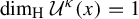 $ \operatorname {\mathrm {\dim _H}}\mathcal U^\kappa (x)=1 $ for
$ \operatorname {\mathrm {\dim _H}}\mathcal U^\kappa (x)=1 $ for 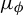 $ \mu _\phi $-almost every (a.e.)
$ \mu _\phi $-almost every (a.e.) 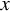 $ x $ is proven to be
$ x $ is proven to be 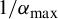 $ 1/\alpha _{\max } $, where
$ 1/\alpha _{\max } $, where 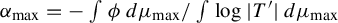 $ \alpha _{\max }=-\int \phi \,d\mu _{\max }/\int \log |T'|\,d\mu _{\max } $ and
$ \alpha _{\max }=-\int \phi \,d\mu _{\max }/\int \log |T'|\,d\mu _{\max } $ and 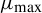 $ \mu _{\max } $ is the Gibbs measure associated with the potential
$ \mu _{\max } $ is the Gibbs measure associated with the potential 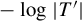 $ -\log |T'| $. Moreover, when
$ -\log |T'| $. Moreover, when 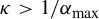 $ \kappa>1/\alpha _{\max } $, we show that for
$ \kappa>1/\alpha _{\max } $, we show that for 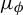 $ \mu _\phi $-a.e.
$ \mu _\phi $-a.e. 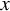 $ x $, the Hausdorff dimension of
$ x $, the Hausdorff dimension of 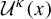 $ \mathcal U^\kappa (x) $ agrees with the multifractal spectrum of
$ \mathcal U^\kappa (x) $ agrees with the multifractal spectrum of 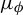 $ \mu _\phi $.
$ \mu _\phi $.