Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-24T17:23:13.812Z Has data issue: false hasContentIssue false
  • English
  • Français

Transversal local rigidity of discrete abelian actions on Heisenberg nilmanifolds

Part of: Dynamical systems with hyperbolic behavior Smooth dynamical systems: general theory

Published online by Cambridge University Press:  04 August 2021

DANIJELA DAMJANOVIĆ  and
JAMES TANIS
DANIJELA DAMJANOVIĆ
Affiliation:
Department of Mathematics, Kungliga Tekniska Högskolan, Lindstedtsvägen 25, 10044 Stockholm, Sweden (e-mail: [email protected])
JAMES TANIS*
Affiliation:
The MITRE Corporation, McLean, VA 22102, USA
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we prove a perturbative result for a class of 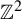${\mathbb Z}^2$ actions on Heisenberg nilmanifolds that have Diophantine properties. Along the way we prove cohomological rigidity and obtain a tame splitting for the cohomology with coefficients in smooth vector fields for such actions.

Keywords

local rigityabelian actionsHeisenberg nilmanifolds

MSC classification

Primary: 37C15: Topological and differentiable equivalence, conjugacy, invariants, moduli, classification 37C85: Dynamics of group actions other than ${bf Z}$ and ${bf R}$, and foliations 37D20: Uniformly hyperbolic systems (expanding, Anosov, Axiom A, etc.)
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 42 , Issue 10 , October 2022 , pp. 3111 - 3151
Copyright
© The MITRE Corporation, 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Cosentino, S. and Flaminio, L.. Equidistribution for higher-rank Abelian actions on Heisenberg nilmanifolds. J. Mod. Dyn. 9(4) (2015), 305–353.CrossRefGoogle Scholar
Damjanović, D.. Perturbations of smooth actions with non-trivial cohomology. Comm. Pure Appl. Math. LXVII (2014), 1391–1417.CrossRefGoogle Scholar
Damjanović, D.. Abelian actions with globally hypoelliptic leafwise Laplacian and rigidity. J. Anal. Math. 129(1) (2016), 139–163.CrossRefGoogle Scholar
Damjanović, D. and Fayad, B.. On local rigidity of partially hyperbolic affine ${\mathbb{Z}}^k$ actions. J. Reine Angew. Math. 751 (2019), 1–26.CrossRefGoogle Scholar
Damjanović, D. and Katok, A.. Local rigidity of partially hyperbolic actions I. KAM method and ${\mathbb{Z}}^k$ actions on the torus. Ann. of Math. (2) 172(3) (2010), 1805–1858.CrossRefGoogle Scholar
Damjanović, D. and Katok, A.. Local rigidity of partially hyperbolic actions II. The geometric method and restrictions of Weyl chamber flows on $\mathrm{SL}\left(n,\mathbb{R}\right)/ \varGamma$ . Int. Math. Res. Not. IMRN 2011(19) (2010), 4405–4430.Google Scholar
Damjanović, D. and Katok, A.. Local rigidity of homogeneous parabolic actions: I. A model case. J. Mod. Dyn. 5(2) (2011), 203–235.CrossRefGoogle Scholar
Damjanović, D. and Tanis, J.. Cocycle rigidity and splitting for some discrete parabolic actions. Discrete Contin. Dyn. Syst. 34(12) (2014), 5211–5227.CrossRefGoogle Scholar
Flaminio, L. and Forni, G.. Equidistribution of nilflows and applications to theta sums. Ergod. Th. & Dynam. Sys. 26(2) (2006), 409–433.CrossRefGoogle Scholar
Hamilton, R. H.. The inverse function theorem of Nash and Moser. Bull. Amer. Math. Soc. (N.S.) 7(1) (1982), 65–222.CrossRefGoogle Scholar
Katok, A. and Spatzier, R. J.. Differential rigidity of Anosov actions of higher rank Abelian groups and algebraic lattice actions. Proc. Steklov Inst. Math. 216 (1997), 287–314.Google Scholar
Moser, J.. On commuting circle mappings and simultaneous Diophantine approximations. Math. Z. 205(1) (1990), 105–121.CrossRefGoogle Scholar
Petkovic, B.. Local rigidity for simultaneous Diophantine translations on tori of arbitrary dimension. Regul. Chaotic Dyn. 26(6) (2021), to appear.CrossRefGoogle Scholar
Tanis, J. and Wang, Z. J.. Cohomological equation and cocycle rigidity of discrete parabolic actions. Discrete Contin. Dyn. Syst. 39(7) (2019), 3969–4000.CrossRefGoogle Scholar
Tanis, J. and Wang, Z. J.. Cohomological equation and cocycle rigidity of discrete parabolic actions in some higher rank Lie groups. J. Anal. Math. 142 (2020), 125–191.CrossRefGoogle Scholar
Tolimieri, R.. Heisenberg manifolds and theta functions. Trans. Amer. Math. Soc. 239 (1978), 293–319.CrossRefGoogle Scholar
Vinhage, K. and Wang, Z. J.. Local rigidity of higher rank homogeneous abelian actions: a complete solution via the geometric method. Geom. Dedicata 200 (2019), 385–439.CrossRefGoogle Scholar
Wang, Z. J.. Local rigidity of parabolic algebraic actions. Preprint, 2019, arXiv:1908.10496.Google Scholar
Wilkinson, A. and Xue, J.. Rigidity of some abelian-by-cyclic solvable group actions on ${T}^N$ . Comm. Math. Phys. 376(3) (2020), 1223–1259.CrossRefGoogle Scholar