Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-28T03:05:51.488Z Has data issue: false hasContentIssue false
  • English
  • Français

Transitivity of surface dynamics lifted to Abelian covers

Published online by Cambridge University Press:  03 February 2009

PHILIP BOYLAND
PHILIP BOYLAND*
Affiliation:
Department of Mathematics, University of Florida, Gainesville, FL 32611-8105, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

A homeomorphism f of a manifold M is called H1-transitive if there is a transitive lift of an iterate of f to the universal Abelian cover 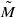. Roughly speaking, this means that f has orbits which repeatedly and densely explore all elements of H1(M). For a rel pseudo-Anosov map ϕ of a compact surface M we show that the following are equivalent: (a) ϕ is H1-transitive, (b) the action of ϕ on H1(M) has spectral radius one and (c) the lifts of the invariant foliations of ϕ to 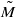have dense leaves. The proof relies on a characterization of transitivity for twisted ℤd-extensions of a transitive subshift of finite type.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 29 , Issue 5 , October 2009 , pp. 1417 - 1449
Copyright
Copyright © Cambridge University Press 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Band, G. and Boyland, P.. Entropy and dynamics in Abelian covering spaces, in preparation.Google Scholar
[2]Band, G. and Boyland, P.. The Burau estimate for the entropy of a braid. Algebra Geom. Topol. 7 (2007), 1345–1378.CrossRefGoogle Scholar
[3]Boyland, P., Guaschi, J. and Hall, T.. L’ensemble de rotation des homéomorphismes pseudo-Anosov. C. R. Acad. Sci. Paris Sér. I Math. 316(10) (1993), 1077–1080.Google Scholar
[4]Boyland, P.. Topological methods in surface dynamics. Topology Appl. 58(3) (1994), 223–298.CrossRefGoogle Scholar
[5]Casson, A. J. and Bleiler, S. A.. Automorphisms of surfaces after Nielsen and Thurston (London Mathematical Society Student Texts, 9). Cambridge University Press, Cambridge, 1988.CrossRefGoogle Scholar
[6]Cerbelli, S. and Giona, M.. A continuous archetype of nonuniform chaos in area-preserving dynamical systems. J. Nonlinear Sci. 15(6) (2005), 387–421.CrossRefGoogle Scholar
[7]Coudene, Y.. Topological dynamics and local product structure. J. London Math. Soc. (2) 69(2) (2004), 441–456.CrossRefGoogle Scholar
[8]Doeff, E. and Misiurewicz, M.. Shear rotation numbers. Nonlinearity 10(6) (1997), 1755–1762.CrossRefGoogle Scholar
[9]Erik Doeff, H.. Rotation measures for homeomorphisms of the torus homotopic to a Dehn twist. Ergod. Th. & Dynam. Sys. 17(3) (1997), 575–591.CrossRefGoogle Scholar
[10]Farb, Benson. Some problems on mapping class groups and moduli space. Problems on Mapping Class Groups and Related Topics (Proceedings of Symposia in Pure Mathematics, 74). American Mathematical Society, Providence, RI, 2006, pp. 11–55.CrossRefGoogle Scholar
[11]Fathi, A., Lauderbach, F. and Poenaru, V.. Travaux de Thurston sur les surfaces. Séminaire Orsay (Astérisque, 66–67). Société Mathématique de France, Paris, 1991. (Reprint of Travaux de Thurston sur les surfaces, 1979.)Google Scholar
[12]Fried, D.. Flow equivalence, hyperbolic systems and a new zeta function for flows. Comment. Math. Helv. 57(2) (1982), 237–259.CrossRefGoogle Scholar
[13]Fried, D.. The geometry of cross sections to flows. Topology 21(4) (1982), 353–371.CrossRefGoogle Scholar
[14]Fried, D.. Periodic points and twisted coefficients. Geometric Dynamics (Rio de Janeiro, 1981) (Lecture Notes in Mathematics, 1007). Springer, Berlin, 1983, pp. 261–293.CrossRefGoogle Scholar
[15]Fried, D.. Entropy and twisted cohomology. Topology 25(4) (1986), 455–470.CrossRefGoogle Scholar
[16]Gottschalk, W. H. and Hedlund, G. A.. Topological Dynamics (American Mathematical Society Colloquium Publications, 36). American Mathematical Society, Providence, RI, 1955.CrossRefGoogle Scholar
[17]Guivarc’h, Y.. Propriétés ergodiques, en mesure infinie, de certains systèmes dynamiques fibrés. Ergod. Th. & Dynam. Sys. 9(3) (1989), 433–453.CrossRefGoogle Scholar
[18]Handel, M.. Global shadowing of pseudo-Anosov homeomorphisms. Ergod. Th. & Dynam. Sys. 5(3) (1985), 373–377.CrossRefGoogle Scholar
[19]Jenkinson, O.. Rotation, entropy, and equilibrium states. Trans. Amer. Math. Soc. 353(9) (2001), 3713–3739 electronic.CrossRefGoogle Scholar
[20]Johnson, D.. A survey of the Torelli group. Low-dimensional Topology (San Francisco, CA, 1981) (Contemporary Mathematics, 20). American Mathematical Society, Providence, RI, 1983,pp. 165–179.CrossRefGoogle Scholar
[21]Kitchens, B. P.. One-sided, two-sided and countable state Markov shifts. Symbolic Dynamics (Universitext). Springer, Berlin, 1998.CrossRefGoogle Scholar
[22]Kwapisz, J.. Rotation sets and entropy. PhD Thesis, SUNY at Stony Brook, 1995.Google Scholar
[23]MacKay, R. S.. Cerbelli and Giona’s map is pseudo-Anosov and nine consequences. J. Nonlinear Sci. 16(4) (2006), 415–434.CrossRefGoogle Scholar
[24]Marcus, D. A.. Number Fields (Universitext). Springer, New York, 1977.CrossRefGoogle Scholar
[25]Mentzen, M. K.. Group Extension of Dynamical Systems in Ergodic Theory and Topological Dynamics (Lecture Notes in Nonlinear Analysis, 6). Juliusz Schauder Center for Nonlinear Studies, Toruń, 2005.Google Scholar
[26]Marcus, B. and Tuncel, S.. The weight-per-symbol polytope and scaffolds of invariants associated with Markov chains. Ergod. Th. & Dynam. Sys. 11(1) (1991), 129–180.CrossRefGoogle Scholar
[27]Newman, M.. Integral Matrices (Pure and Applied Mathematics, 45). Academic Press, New York, 1972.Google Scholar
[28]Nitica, V.. Examples of topologically transitive skew-products. Discrete Contin. Dynam. Syst. 6(2) (2000), 351–360.CrossRefGoogle Scholar
[29]Parwani, K.. Simple periodic orbits on surfaces. PhD Thesis, Northwestern University, 2003.Google Scholar
[30]Parry, W. and Pollicott, M.. Skew products and Livsic Theory. Representation Theory, Dynamical Systems, and Asymptotic Combinatorics (American Mathematical Society Translations Series 2, 217). American Mathematical Society, Providence, RI, 2006, pp. 139–165.Google Scholar
[31]Pollicott, M. and Sharp, R.. Pseudo-Anosov foliations on periodic surfaces. Topology Appl. 154(12) (2007), 2365–2375.CrossRefGoogle Scholar
[32]Pinsky, T. and Wajnryb, B.. Dynamics of shear homeomorphisms of tori and the Bestvina-Handel algorithm. Preprint (2007), arXiv:0704.1272.Google Scholar
[33]Rees, M.. Checking ergodicity of some geodesic flows with infinite Gibbs measure. Ergod. Th. & Dynam. Sys. 1(1) (1981), 107–133.CrossRefGoogle Scholar
[34]Thurston, W. P.. On the geometry and dynamics of diffeomorphisms of surfaces. Bull. Amer. Math. Soc. (N.S.) 19(2) (1988), 417–431.CrossRefGoogle Scholar
[35]Ziemian, K.. Rotation sets for subshifts of finite type. Fund. Math. 146(2) (1995), 189–201.CrossRefGoogle Scholar