Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-24T02:25:01.906Z Has data issue: false hasContentIssue false
  • English
  • Français

Transfer operators for ultradifferentiable expanding maps of the circle

Part of: Smooth dynamical systems: general theory

Published online by Cambridge University Press:  11 June 2020

MALO JÉZÉQUEL
MALO JÉZÉQUEL*
Affiliation:
Laboratoire de Probabilités, Statistique et Modélisation (LPSM), CNRS, Sorbonne Université, Université de Paris, 4, Place Jussieu, 75005Paris, France email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a 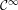${\mathcal{C}}^{\infty }$ expanding map $T$ of the circle, we construct a Hilbert space 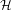${\mathcal{H}}$ of smooth functions on which the transfer operator 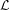${\mathcal{L}}$ associated to $T$ acts as a compact operator. This result is made quantitative (in terms of singular values of the operator 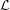${\mathcal{L}}$ acting on 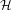${\mathcal{H}}$) using the language of Denjoy–Carleman classes. Moreover, the nuclear power decomposition of Baladi and Tsujii can be performed on the space 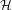${\mathcal{H}}$, providing a bound on the growth of the dynamical determinant associated to 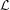${\mathcal{L}}$.

Keywords

transfer operatordynamical determinantRuelle resonancesDenjoy–Carleman classes

MSC classification

Primary: 37C30: Zeta functions, (Ruelle-Frobenius) transfer operators, and other functional analytic techniques in dynamical systems
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 7 , July 2021 , pp. 2049 - 2068
Check for updates
Copyright
© The Author(s) 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baladi, V.. Dynamical Zeta Functions and Dynamical Determinants for Hyperbolic Maps (Ergebnisse der Mathematik und ihrer Grenzgebiete, 68) . Springer, Berlin, 2018.CrossRefGoogle Scholar
Baladi, V. and Tsujii, M.. Dynamical determinants and spectrum for hyperbolic diffemorphisms. Geometric and Probabilistic Structures in Dynamics (Contemporary Mathematics, 469) . American Mathematical Society, Providence, RI, 2008, pp. 29–68.CrossRefGoogle Scholar
Bandtlow, O. F.. Resolvent estimates for operators belonging to exponential classes. Integral Equations Operator Theory 61(1) (2008), 21–43.CrossRefGoogle Scholar
Bandtlow, O. F. and Jenkinson, O.. Explicit eigenvalue estimates for transfer operators acting on spaces of holomorphic functions. Adv. Math. 218(3) (2008), 902–925.CrossRefGoogle Scholar
Bandtlow, O. F., Just, W. and Slipantschuk, J.. Spectral structure of transfer operators for expanding circle maps. Ann. Inst. H. Poincaré Anal. Non Linéaire 34(1) (2017), 31–43.CrossRefGoogle Scholar
Bandtlow, O. F. and Naud, F.. Lower bounds for the Ruelle spectrum of analytic expanding circle maps. Ergod. Th. & Dynam. Sys. 39(2) (2019), 289–310.CrossRefGoogle Scholar
Boas, R.. Entire Functions. Academic Press, New York, 1954.Google Scholar
Fürdös, S., Nenning, D. N., Rainer, A. and Schindl, G.. Almost analytic extensions of ultradifferentiable functions with applications to microlocal analysis. J. Math. Anal. Appl. 481(1) (2020),123451.CrossRefGoogle Scholar
Gohberg, I., Goldberg, S. and Krupnik, N.. Traces and Determinants of Linear Operators (Operator Theory: Advances and Applications, 116) . Birkhaüser, Basel, 2000.CrossRefGoogle Scholar
Gouëzel, S. and Liverani, C.. Compact locally maximal hyperbolic sets for smooth maps: fine statistical properties. J. Differential Geom. 79(3) (2008), 433–477.CrossRefGoogle Scholar
Grothendieck, A.. Produits tensoriels topologiques et espaces nucléaires (Memoirs of the American Mathematical Society, 16) . American Mathematical Society, Providence, RI, 1955.CrossRefGoogle Scholar
Jézéquel, M.. Global trace formula for ultra-differentiable Anosov flows. Preprint, 2019, arXiv:1901.09576 [math].Google Scholar
Jézéquel, M.. Local and global trace formulae for smooth hyperbolic diffeomorphisms. J. Spectr. Theory 10(1) (2020), 185–249.CrossRefGoogle Scholar
Kato, T.. Perturbation Theory for Linear Operators. Springer, Berlin, 1966.Google Scholar
Kriegl, A., Michor, P. W. and Rainer, A.. The convenient setting for non-quasianalytic Denjoy–Carleman differentiable mappings. J. Funct. Anal. 256(11) (2009), 3510–3544.CrossRefGoogle Scholar
Kuroda, S. T.. On a generalization of the Weinstein–Aronszajn formula and the infinite determinant. Sci. Papers College Gen. Ed. Univ. Tokyo 11 (1961), 1–12.Google Scholar
Naud, F.. The Ruelle spectrum of generic transfer operators. Discrete Contin. Dyn. Syst. Ser. A 32(7) (2012), 2521–2531.CrossRefGoogle Scholar
Ruelle, D.. Zeta-functions for expanding maps and Anosov flows. Invent. Math. 34 (1976), 231–242.CrossRefGoogle Scholar
Slipantschuk, J., Bandtlow, O. F. and Just, W.. Analytic expanding circle maps with explicit spectra. Nonlinearity 26(12) (2013), 3231–3245.CrossRefGoogle Scholar
Slipantschuk, J., Bandtlow, O. F. and Just, W.. Complete spectral data for analytic Anosov maps of the torus. Nonlinearity 30(7) (2017), 2667–2686.CrossRefGoogle Scholar