Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-04T19:16:02.831Z Has data issue: false hasContentIssue false
  • English
  • Français

Topological structure and entropy of mixing graph maps

Published online by Cambridge University Press:  30 April 2013

GRZEGORZ HARAŃCZYK ,
DOMINIK KWIETNIAK  and
PIOTR OPROCHA
GRZEGORZ HARAŃCZYK
Affiliation:
Institute of Mathematics, Faculty of Mathematics and Computer Science, Jagiellonian University in Kraków, Łojasiewicza 6, 30-348 Kraków, Poland email [email protected]@uj.edu.pl
DOMINIK KWIETNIAK
Affiliation:
Institute of Mathematics, Faculty of Mathematics and Computer Science, Jagiellonian University in Kraków, Łojasiewicza 6, 30-348 Kraków, Poland email [email protected]@uj.edu.pl
PIOTR OPROCHA
Affiliation:
Faculty of Applied Mathematics, AGH University of Science and Technology, al. Mickiewicza 30, 30-059 Kraków, Poland email [email protected] Institute of Mathematics, Polish Academy of Sciences, ul. Śniadeckich 8, 00-956 Warszawa, Poland
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 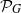${ \mathcal{P} }_{G} $ be the family of all topologically mixing, but not exact self-maps of a topological graph 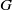$G$. It is proved that the infimum of topological entropies of maps from 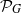${ \mathcal{P} }_{G} $ is bounded from below by 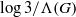$\log 3/ \Lambda (G)$, where 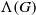$\Lambda (G)$ is a constant depending on the combinatorial structure of 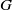$G$. The exact value of the infimum on 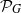${ \mathcal{P} }_{G} $ is calculated for some families of graphs. The main tool is a refined version of the structure theorem for mixing graph maps. It also yields new proofs of some known results, including Blokh’s theorem (topological mixing implies the specification property for maps on graphs).

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 34 , Issue 5 , October 2014 , pp. 1587 - 1614
Copyright
Copyright ©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alsedà, Ll., Baldwin, S., Llibre, J. and Misiurewicz, M.. Entropy of transitive tree maps. Topology 36 (2) (1997), 519–532.Google Scholar
Alsedà, Ll., del Río, M. A. and Rodríguez, J. A.. A splitting theorem for transitive maps. J. Math. Anal. Appl. 232 (2) (1999), 359–375.Google Scholar
Alsedà, Ll., del Río, M. A. and Rodríguez, J. A.. Transitivity and dense periodicity for graph maps. J. Difference Equ. Appl. 9 (6) (2003), 577–598.Google Scholar
Alsedà, Ll., Kolyada, S., Llibre, J. and Snoha, L’.. Entropy and periodic points for transitive maps. Trans. Amer. Math. Soc. 351 (4) (1999), 1551–1573.Google Scholar
Alsedà, Ll., Llibre, J. and Misiurewicz, M.. Combinatorial Dynamics and Entropy in Dimension One (Advanced Series in Nonlinear Dynamics, 5), 2nd edn. World Scientific, River Edge, NJ, 2000.Google Scholar
Baldwin, S.. Entropy estimates for transitive maps on trees. Topology 40 (3) (2001), 551–569.Google Scholar
Balibrea, F. and Snoha, L’.. Topological entropy of Devaney chaotic maps. Topology Appl. 133 (3) (2003), 225–239.Google Scholar
Banks, J.. Regular periodic decompositions for topologically transitive maps. Ergod. Th. & Dynam. Sys. 17 (3) (1997), 505–529.Google Scholar
Banks, J. and Trotta, B.. Weak mixing implies mixing for maps on topological graphs. J. Difference Equ. Appl. 11 (12) (2005), 1071–1080.Google Scholar
Blanchard, F.. Topological chaos: What may this mean? J. Difference Equ. Appl. 15 (1) (2009), 23–46.Google Scholar
Block, L., Guckenheimer, J., Misiurewicz, M. and Young, L. S.. Periodic points and topological entropy of one dimensional maps. Global Theory of Dynamical Systems (Lecture Notes in Mathematics, 819). Springer, Berlin, 1980, pp. 18–34.Google Scholar
Blokh, A. M.. Dynamical systems on one-dimensional branched manifolds. I. Teor. Funktsiĭ Funktsional. Anal. i Prilozhen. (46) (1986), 8–18.Google Scholar
Blokh, A. M.. Dynamical systems on one-dimensional branched manifolds. II. Teor. Funktsiĭ Funktsional. Anal. i Prilozhen. (47) (1987), 67–77.Google Scholar
Blokh, A. M.. Dynamical systems on one-dimensional branched manifolds. III. Teor. Funktsiĭ Funktsional. Anal. i Prilozhen. (48) (1987), 32–46.Google Scholar
Bowen, R.. Periodic points and measures for axiom A-diffeomorphisms. Trans. Amer. Math. Soc. 154 (1971), 377–397.Google Scholar
Buzzi, J.. Specification on the interval. Trans. Amer. Math. Soc. 349 (7) (1997), 2737–2754.Google Scholar
Coven, E. M. and Mulvey, I.. Transitivity and the centre for maps of the circle. Ergod. Th. & Dynam. Sys. 6 (1) (1986), 1–8.Google Scholar
Croom, F. H.. Basic Concepts of Algebraic Topology (Undergraduate Texts in Mathematics, 51). Springer, New York, 1978.Google Scholar
Dirbák, M.. Extensions of dynamical systems without increasing the entropy. Nonlinearity 21 (11) (2008), 2693–2713.Google Scholar
Dirbák, M., Snoha, L’. and Špitalský, V.. Minimality, transitivity, mixing and topological entropy on spaces with a free interval. Ergod. Th. & Dynam. Sys., to appear, doi 10.1017/S0143385712000442, published online 21 August 2012.Google Scholar
Harańczyk, G. and Kwietniak, D.. When lower entropy implies stronger Devaney chaos. Proc. Amer. Math. Soc. 137 (6) (2009), 2063–2073.Google Scholar
Harańczyk, G., Kwietniak, D. and Oprocha, P.. A note on transitivity, sensitivity and chaos for graph maps. J. Difference Equ. Appl. 17 (10) (2011), 1549–1553.Google Scholar
Kato, H.. Concerning continuum-wise fully expansive homeomorphisms of continua. Topology Appl. 53 (3) (1993), 239–258.Google Scholar
Kolyada, S. and Snoha, L’.. Some aspects of topological transitivity—a survey. Grazer Math. Ber. 334 (1997), 3–35.Google Scholar
Kościelniak, P., Oprocha, P. and Tuncali, M.. Hereditary indecomposable inverse limits of graphs: shadowing, mixing and exactness. Proc. Amer. Math. Soc., to appear.Google Scholar
Kwietniak, D. and Misiurewicz, M.. Exact Devaney chaos and entropy. Qual. Theory Dyn. Syst. 6 (1) (2005), 169–179.Google Scholar
Kwietniak, D. and Oprocha, P.. Topological entropy and chaos for maps induced on hyperspaces. Chaos Solitons Fractals 33 (2007), 76–86.Google Scholar
Lind, D. and Marcus, B.. An Introduction to Symbolic Dynamics and Coding. Cambridge University Press, Cambridge, 1995.Google Scholar
Moise, E. E.. Geometric Topology in Dimensions 2 and 3 (Graduate Texts in Mathematics, 47). Springer, New York, 1977.Google Scholar
Nadler, S. B. Jr. Continuum theory and graph theory: disconnection numbers. J. Lond. Math. Soc. (2) 47 (1) (1993), 167–181.Google Scholar
Oprocha, P. and Zhang, G.. Dimensional entropy over sets and fibres. Nonlinearity 24 (8) (2011), 2325–2346.Google Scholar
Parry, W.. Symbolic dynamics and transformations of the unit interval. Trans. Amer. Math. Soc. 122 (1966), 368–378.Google Scholar
Robinson, C.. Dynamical Systems (Studies in Advanced Mathematics, 28), 2nd edn. CRC Press, Boca Raton, FL, 1999.Google Scholar
Su, Y. and Ye, X.. Topological entropy of a class of transitive maps of a tree. Topology Proc. 24 (Summer) (1999), 597–609.Google Scholar
Špitalský, V.. Entropy and exact Devaney chaos on totally regular continua. Discrete Contin. Dyn. Syst. A 33 (7) (2013), 3135–3152.Google Scholar
Ye, X.. Non-wandering points and the depth of a graph map. J. Aust. Math. Soc. A 69 (2) (2000), 143–152.Google Scholar
Ye, X.. Topological entropy of transitive maps of a tree. Ergod. Th. & Dynam. Sys. 20 (1) (2000), 289–314.CrossRefGoogle Scholar
Yokoi, K.. Strong transitivity and graph maps. Bull. Pol. Acad. Sci. Math. 53 (2005), 377–388.Google Scholar