Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-19T04:44:29.223Z Has data issue: false hasContentIssue false
  • English
  • Français

The topological strong spatial mixing property and new conditions for pressure approximation

Published online by Cambridge University Press:  04 May 2017

RAIMUNDO BRICEÑO
RAIMUNDO BRICEÑO*
Affiliation:
Department of Mathematics, University of British Columbia, 1984 Mathematics Road V6T 1Z2, Vancouver, B.C., Canada email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In the context of stationary 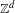$\mathbb{Z}^{d}$ nearest-neighbour Gibbs measures $\unicode[STIX]{x1D707}$ satisfying strong spatial mixing, we present a new combinatorial condition (the topological strong spatial mixing property) on the support of $\unicode[STIX]{x1D707}$ that is sufficient for having an efficient approximation algorithm for topological pressure. We establish many useful properties of topological strong spatial mixing for studying strong spatial mixing on systems with hard constraints. We also show that topological strong spatial mixing is, in fact, necessary for strong spatial mixing to hold at high rate. Part of this work is an extension of results obtained by Gamarnik and Katz [Sequential cavity method for computing free energy and surface pressure. J. Stat. Phys.137(2) (2009), 205–232], and Marcus and Pavlov [An integral representation for topological pressure in terms of conditional probabilities. Israel J. Math.207(1) (2015), 395–433], who gave a special representation of topological pressure in terms of conditional probabilities.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 5 , August 2018 , pp. 1658 - 1696
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Balister, P., Bollobás, B. and Quas, A.. Entropy along convex shapes, random tilings and shifts of finite type. Illinois J. Math. 46(3) (2002), 781–795.CrossRefGoogle Scholar
van den Berg, J.. A uniqueness condition for Gibbs measures, with application to the 2-dimensional Ising antiferromagnet. Comm. Math. Phys. 152(1) (1993), 161–166.Google Scholar
van den Berg, J. and Maes, C.. Disagreement percolation in the study of Markov fields. Ann. Probab. 22(2) (1994), 749–763.Google Scholar
Berger, R.. The Undecidability of the Domino Problem, vol. 66. American Mathematical Society, 1966.Google Scholar
Boyle, M., Pavlov, R. and Schraudner, M.. Multidimensional sofic shifts without separation and their factors. Trans. Amer. Math. Soc. 362(9) (2010), 4617–4653.Google Scholar
Brightwell, G. R. and Winkler, P.. Gibbs measures and dismantlable graphs. J. Combin. Theory Ser. B 78(1) (2000), 141–166.CrossRefGoogle Scholar
Burton, R. and Steif, J.. Non-uniqueness of measures of maximal entropy for subshifts of finite type. Ergod. Th. & Dynam. Sys. 14(02) (1994), 213–235.Google Scholar
Chandgotia, N. and Meyerovitch, T.. Markov Random fields, Markov cocycles and the 3-colored chessboard. Israel J. Math. 215(2) (2016), 909–964.CrossRefGoogle Scholar
Friedland, S.. On the entropy of ℤ d subshifts of finite type. Linear Algebra Appl. 252 (1997), 199–220.CrossRefGoogle Scholar
Gamarnik, D. and Katz, D.. Sequential cavity method for computing free energy and surface pressure. J. Stat. Phys. 137(2) (2009), 205–232.Google Scholar
Gamarnik, D., Katz, D. and Misra, S.. Strong spatial mixing of list coloring of graphs. Random Structures Algorithms 46(4) (2015), 599–613.CrossRefGoogle Scholar
Georgii, H.-O.. Gibbs Measures and Phase Transitions (De Gruyter Studies in Mathematics, 9) , 2nd edn. de Gruyter, Berlin, 2011.Google Scholar
Goldberg, L. A., Martin, R. and Paterson, M.. Strong spatial mixing with fewer colous for lattice graphs. SIAM J. Comput. 35(2) (2005), 486–517.CrossRefGoogle Scholar
Goldberg, L. A. et al. . Improved mixing bounds for the anti-ferromagnetic Potts model on ℤ2 . LMS J. Comput. Math. 9 (2006), 1–20.Google Scholar
Hochman, M. and Meyerovitch, T.. A characterization of the entropies of multidimensional shifts of finite type. Ann. of Math. (2) 171(3) (2010), 2011–2038.Google Scholar
den Hollander, F. and Steif, J.. On K-automorphisms, Bernoulli shifts and Markov random fields. Ergod. Th. & Dynam. Sys. 17(02) (1997), 405–415.Google Scholar
Kasteleyn, P. W.. The statistics of dimers on a lattice: I. The number of dimer arrangements on a quadratic lattice. Physica 27(12) (1961), 1209–1225.Google Scholar
Keller, G.. Equilibrium States in Ergodic Theory. Cambridge University Press, Cambridge, 1998.Google Scholar
Ko, K.-I.. Complexity Theory of Real Functions (Progress in Theoretical Computer Science) . Birkhäuser, Boston, 1991.CrossRefGoogle Scholar
Krengel, U. and Brunel, A.. Ergodic Theorems. de Gruyter Studies in Mathematics. de Gruyter, Berlin, 1985.CrossRefGoogle Scholar
Lieb, E. H.. Exact solution of the problem of the entropy of two-dimensional ice. Phys. Rev. Lett. 18(17) (1967), 692–694.Google Scholar
Lightwood, S.. Morphisms from non-periodic ℤ2 subshifts I: constructing embeddings from homomorphisms. Ergod. Th. & Dynam. Sys. 23(02) (2003), 587–609.Google Scholar
Lind, D. and Marcus, B.. An Introduction to Symbolic Dynamics and Coding. Cambridge University Press, Cambridge, 1995.Google Scholar
Lindvall, T.. Lectures on the Coupling Method. Wiley Series in Probability and Mathematical Statistics (A Wiley-Interscience Publication) . Wiley, New York, 1992.Google Scholar
Loomis, L. H. and Whitney, H.. An inequality related to the isoperimetric inequality. Bull. Amer. Math. Soc. (N.S.) 55(10) (1949), 961–962.Google Scholar
Marcus, B. and Pavlov, R.. Computing bounds for entropy of stationary ℤ d Markov random fields. SIAM J. Discrete Math. 27(3) (2013), 1544–1558.Google Scholar
Marcus, B. and Pavlov, R.. An integral representation for topological pressure in terms of conditional probabilities. Israel J. Math. 207(1) (2015), 395–433.Google Scholar
Martinelli, F.. Lectures on Glauber dynamics for discrete spin models. English. Lectures on Probability Theory and Statistics (Lecture Notes in Mathematics, 1717) . Ed. Bernard, P.. Springer, Berlin, 1999, pp. 93–191.Google Scholar
Martinelli, F., Olivieri, E. and Schonmann, R. H.. For 2-D lattice spin systems weak mixing implies strong mixing. Comm. Math. Phys. 165(1) (1994), 33–47.Google Scholar
Misiurewicz, M.. A short proof of the variational principle for a ℤ+ N action on a compact space. Int. Conf. on Dynamical Systems in Mathematical Physics, Astérisque. vol. 40 Société Mathématique de France, Paris, 1976, pp. 147–157.Google Scholar
Pavlov, R.. Approximating the hard square entropy constant with probabilistic methods. Ann. Probab. 40(6) (2012), 2362–2399.Google Scholar
Robinson, R. M.. Undecidability and nonperiodicity for tilings of the plane. Invent. Math. 12 (1971), 177–209.Google Scholar
Ruelle, D.. Thermodynamic Formalism. The Mathematical Structure of Equilibrium Statistical Mechanics (Cambridge Mathematical Library) . 2nd edn. Cambridge University Press, Cambridge, 2004.Google Scholar
Salas, J. and Sokal, A.. Absence of phase transition for antiferromagnetic Potts models via the Dobrushin uniqueness theorem. J. Stat. Phys. 86(3–4) (1997), 551–579.Google Scholar
Walters, P.. An Introduction to Ergodic Theory (Graduate Texts in Mathematics, 79) . Springer, Berlin, 1982.Google Scholar
Ward, T.. Automorphisms of ℤ d -subshifts of finite type. Indag. Math. (N.S.) 5(4) (1994), 495–504.Google Scholar
Weitz, D.. Combinatorial criteria for uniqueness of Gibbs measures. Random Structures Algorithms 27(4) (2005), 445–475.Google Scholar
Weitz, D.. Counting independent sets up to the tree threshold. Proc. Thirty-eighth Annual ACM Symposium on Theory of Computing (STOC,06). ACM, Seattle, WA, 2006, pp. 140–149.Google Scholar