Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-12-01T01:22:20.688Z Has data issue: false hasContentIssue false
  • English
  • Français

A topological lens for a measure-preserving system

Published online by Cambridge University Press:  02 February 2010

E. GLASNER ,
M. LEMAŃCZYK  and
B. WEISS
E. GLASNER
Affiliation:
Department of Mathematics, Tel Aviv University, Tel Aviv, Israel (email: [email protected])
M. LEMAŃCZYK
Affiliation:
Faculty of Mathematics and Computer Science, Nicolaus Copernicus University, Chopina 12/18, 87-100 Toruń, Poland (email: [email protected])
B. WEISS
Affiliation:
Institute of Mathematics, Hebrew University of Jerusalem, Jerusalem, Israel (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We introduce a functor which associates to every measure-preserving system (X,ℬ,μ,T) a topological system 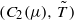defined on the space of twofold couplings of μ, called the topological lens of T. We show that often the topological lens ‘magnifies’ the basic measure dynamical properties of T in terms of the corresponding topological properties of 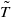. Some of our main results are as follows: (i) T is weakly mixing if and only if 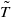is topologically transitive (if and only if it is topologically weakly mixing); (ii) T has zero entropy if and only if 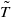has zero topological entropy, and T has positive entropy if and only if 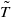has infinite topological entropy; (iii) for T a K-system, the topological lens is a P-system (i.e. it is topologically transitive and the set of periodic points is dense; such systems are also called chaotic in the sense of Devaney).

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 31 , Issue 1 , February 2011 , pp. 49 - 75
Copyright
Copyright © Cambridge University Press 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Glasner, E. and Weiss, B.. On the interplay between measurable and topological dynamics. Handbook of Dynamical Systems, Vol. 1B. Elsevier B.V., Amsterdam, 2006, pp. 597–648.CrossRefGoogle Scholar
[2]Cornfeld, I. P., Fomin, S. V. and Sinai, Ya. G.. Ergodic Theory. Springer, New York, 1982.CrossRefGoogle Scholar
[3]Danilenko, A.. On simplicity concepts for ergodic actions. J. Anal. Math. 102 (2007), 77–117.CrossRefGoogle Scholar
[4]Ellis, R. and Nerurkar, M.. Weakly almost periodic flows. Trans. Amer. Math. Soc. 313 (1989), 103–119.CrossRefGoogle Scholar
[5]Fathi, A.. Le groupe de transformations de [0,1] qui preservent la measure de Lebesgue est un groupe simple. Israel J. Math. 29 (1978), 302–308.CrossRefGoogle Scholar
[6]Furstenberg, H.. Recurrence in Ergodic Theory and Combinatorial Number Theory. Princeton University Press, Princeton, NJ, 1981.CrossRefGoogle Scholar
[7]Glasner, E.. Ergodic Theory via Joinings (Mathematical Surveys and Monographs, 101). American Mathematical Society, Providence, RI, 2003.CrossRefGoogle Scholar
[8]Glasner, E. and King, J.. A zero–one law for dynamical properties. Topological Dynamics and Applications (Minneapolis, MN, 1995) (Contemporary Mathematics, 215). American Mathematical Society, Providence, RI, 1998, pp. 231–242.CrossRefGoogle Scholar
[9]Glasner, E. and Weiss, B.. Sensitive dependence on initial conditions. Nonlinearity 6 (1993), 1067–1075.CrossRefGoogle Scholar
[10]del Junco, A. and Rudolph, D. J.. On ergodic actions whose self-joinings are graphs. Ergod. Th. & Dynam. Sys. 7 (1987), 531–557.CrossRefGoogle Scholar
[11]Kechris, A. S. and Rosendal, C.. Turbulence, amalgamation and generic automorphisms of homogeneous structures. Proc. Lond. Math. Soc. (3) 94 (2007), 302–350.CrossRefGoogle Scholar
[12]Kieffer, J. C.. A simple development of the Thouvenot relative isomorphism theory. Ann. Probab. 12 (1984), 204–211.CrossRefGoogle Scholar
[13]Kǔshnirenko, A. G.. Metric invariants of entropy type. Uspekhi Mat. Nauk 22(5) (1967), 57–65, 137, in Russian.Google Scholar
[14]Lemańczyk, M., Parreau, F. and Thouvenot, J.-P.. Gaussian automorphisms whose ergodic self-joinings are Gaussian. Fund. Math. 164 (2000), 253–293.CrossRefGoogle Scholar
[15]Ornstein, D.. Bernoulli shifts with the same entropy are isomorphic. Adv. Math. 4 (1970), 337–352.CrossRefGoogle Scholar
[16]Ornstein, D.. Ergodic Theory, Randomness, and Dynamical Systems (James K. Whittemore Lectures in Mathematics given at Yale University, Yale Mathematical Monographs, 5). Yale University Press, New Haven, CT, 1974.Google Scholar
[17]Thouvenot, J.-P.. Quelques propriétés des systèmes dynamiques qui se décomposent en un produit de deux systm̀es dont l’un est un schéma de Bernoulli. Israel J. Math. 21 (1975), 177–207.CrossRefGoogle Scholar
[18]Zimmer, R. J.. Extensions of ergodic group actions. Illinois J. Math. 20 (1976), 373–409.CrossRefGoogle Scholar
[19]Zimmer, R. J.. Ergodic actions with generalized discrete spectrum. Illinois J. Math. 20 (1976), 555–588.CrossRefGoogle Scholar