Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T19:59:13.674Z Has data issue: false hasContentIssue false
  • English
  • Français

A Tits alternative for topological full groups

Part of: Topological dynamics Smooth dynamical systems: general theory Abstract harmonic analysis Special aspects of infinite or finite groups

Published online by Cambridge University Press:  27 August 2019

NÓRA GABRIELLA SZŐKE Open the ORCID record for NÓRA GABRIELLA SZŐKE [Opens in a new window]
NÓRA GABRIELLA SZŐKE*
Affiliation:
Institut Fourier, Université Grenoble Alpes, France email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove a Tits alternative for topological full groups of minimal actions of finitely generated groups. On the one hand, we show that topological full groups of minimal actions of virtually cyclic groups are amenable. By doing so, we generalize the result of Juschenko and Monod for 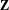$\mathbf{Z}$-actions. On the other hand, when a finitely generated group 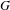$G$ is not virtually cyclic, then we construct a minimal free action of 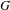$G$ on a Cantor space such that the topological full group contains a non-abelian free group.

Keywords

group actionstopological dynamics

MSC classification

Primary: 37B05: Transformations and group actions with special properties (minimality, distality, proximality, etc.) 43A07: Means on groups, semigroups, etc.; amenable groups
Secondary: 20F65: Geometric group theory 37C85: Dynamics of group actions other than ${bf Z}$ and ${bf R}$, and foliations
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 2 , February 2021 , pp. 622 - 640
Check for updates
Copyright
© Cambridge University Press, 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Elek, G. and Monod, N.. On the topological full group of a minimal Cantor ℤ2 -system. Proc. Amer. Math. Soc. 141 (2013), 3549–3552.CrossRefGoogle Scholar
Giordano, T., Putnam, I. F. and Skau, C. F.. Full groups of Cantor minimal systems. Israel J. Math. 111 (1999), 285–320.10.1007/BF02810689CrossRefGoogle Scholar
Juschenko, K. and de la Salle, M.. Invariant means for the wobbling group. Bull. Belg. Math. Soc. Simon Stevin 22 (2015), 281–290.10.36045/bbms/1432840864CrossRefGoogle Scholar
Juschenko, K., Matte Bon, N., Monod, N. and de la Salle, M.. Extensive amenability and an application to interval exchanges. Ergod. Th. & Dynam. Sys. 38 (2018), 195–219.10.1017/etds.2016.32CrossRefGoogle Scholar
Juschenko, K. and Monod, N.. Cantor systems, piecewise translations and simple amenable groups. Ann. of Math. (2) 178 (2013), 775–787.CrossRefGoogle Scholar
Juschenko, K., Nekrashevych, V. and de la Salle, M.. Extensions of amenable groups by recurrent groupoids. Invent. Math. 206 (2016), 837–867.10.1007/s00222-016-0664-6CrossRefGoogle Scholar
Justin, J.. Groupes et semi-groupes à croissance linéaire. C. R. Math. Acad. Sci. Paris 273 (1971), 212–214.Google Scholar
Lyons, R. and Peres, Y.. Probability on Trees and Networks (Cambridge Series in Statistical and Probabilistic Mathematics, 42) . Cambridge University Press, New York, NY, USA, 2017.Google Scholar
Matui, H.. Some remarks on topological full groups of Cantor minimal systems. Internat. J. Math. 17 (2006), 231–251.10.1142/S0129167X06003448CrossRefGoogle Scholar
Matui, H.. Homology and topological full groups of étale groupoids on totally disconnected spaces. Proc. Lond. Math. Soc. 104 (2011), 27–56.CrossRefGoogle Scholar
Matui, H.. Topological full groups of one-sided shifts of finite type. J. reine angew. Math. 705 (2015), 35–84.Google Scholar
Nekrashevych, V.. Simple groups of dynamical origin. Ergod. Th. & Dynam. Sys. 39 (2019), 707–732.10.1017/etds.2017.47CrossRefGoogle Scholar
Varopoulos, N. T.. Théorie du potentiel sur des groupes et des variétés. C. R. Math. Acad. Sci. Paris 302 (1986), 203–205.Google Scholar