Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-12-01T01:23:04.406Z Has data issue: false hasContentIssue false
  • English
  • Français

Thermodynamic formalism for a family of non-uniformly hyperbolic horseshoes and the unstable Jacobian

Published online by Cambridge University Press:  17 March 2010

RENAUD LEPLAIDEUR
RENAUD LEPLAIDEUR*
Affiliation:
Laboratoire de Mathématiques, UMR 6205, Université de Bretagne Occidentale, 6 av. Victor Le Gorgeu, CS 93837, F-29238 BREST Cedex 3, France (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article we prove the existence and uniqueness of equilibrium states for the potential 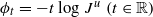and the class of non-uniformly hyperbolic horseshoes which was introduced in Rios [Unfolding homoclinic tangencies inside horseshoes: hyperbolicity, fractal dimensions and persistent tangencies. Nonlinearity14 (2001), 431–462]. We show that the pressure t↦𝒫(t) for −tlog Ju is real-analytic on . We give the exact equations of the two asymptotes to the graph of 𝒫(t) at ±∞ and we prove that these non-uniformly hyperbolic horseshoes do not have measures which minimize the unstable Lyapunov exponent.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 31 , Issue 2 , April 2011 , pp. 423 - 447
Copyright
Copyright © Cambridge University Press 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Bousch, T.. La condition de Walters. Ann. Sci. Éc. Norm. Supér. (4) 34 (2001), 287–311.CrossRefGoogle Scholar
[2]Brémont, J.. Gibbs measures at temperature zero. Nonlinearity 16(2) (2003), 419–426.CrossRefGoogle Scholar
[3]Bruin, H. and Keller, G.. Equilibrium states for S-unimodal maps. Ergod. Th. & Dynam. Sys. 18(4) (1998), 765–789.CrossRefGoogle Scholar
[4]Bruin, H. and Todd, M.. Equilibrium states for interval maps: the potential −tlog ∣df∣. Ann. Sci. Éc. Norm. Supér. (4) 42 (2009), 599–600.Google Scholar
[5]Cao, Y., Luzzatto, S. and Rios, I.. A minimum principle for Lyapunov exponents and a higher-dimensional version of a theorem of Mañé. Qual. Theory Dyn. Syst. 5(2) (2004), 261–273.CrossRefGoogle Scholar
[6]Cao, Y., Luzzatto, S. and Rios, I.. Some non-hyperbolic systems with strictly non-zero Lyapunov exponents for all invariant measures: horseshoes with internal tangencies. Discrete Contin. Dyn. Syst. 15(1) (2006), 61–71.CrossRefGoogle Scholar
[7]Contreras, G., Lopes, A. and Thieullen, P.. Lyapunov minimizing measures for expanding maps of the circle. Ergod. Th. & Dynam. Sys. 21 (2001), 1–31.CrossRefGoogle Scholar
[8]Denker, M., Nitecki, Z. and Urbański, M.. Conformal measures and S-unimodal maps. Dynamical Systems and Applications (World Scientific Series in Applicable Analysis, 4). World Scientific, River Edge, NJ, 1995, pp. 169–212.CrossRefGoogle Scholar
[9]Denker, M. and Urbański, M.. Hausdorff and conformal measures on Julia sets with a rationally indifferent periodic point. J. Lond. Math. Soc. (2) 43(1) (1991), 107–118.CrossRefGoogle Scholar
[10]Leplaideur, R.. Local product structure for equilibrium states. Trans. Amer. Math. Soc. 352(4) (2000), 1889–1912.CrossRefGoogle Scholar
[11]Leplaideur, R.. A dynamical proof for the convergence of Gibbs measures at temperature zero. Nonlinearity 18(6) (2005), 2847–2880.CrossRefGoogle Scholar
[12]Leplaideur, R. and Rios, I.. Invariant manifolds and equilibrium states for non-uniformly hyperbolic horseshoes. Nonlinearity 19(11) (2006), 2667–2694.CrossRefGoogle Scholar
[13]Leplaideur, R. and Rios, I.. On the t-conformal measures and Hausdorff dimension for a family of non-uniformly hyperbolic horseshoes. Ergod. Th. & Dynam. Sys. 29(6) (2009), 1917–1950.CrossRefGoogle Scholar
[14]Makarov, N. and Smirnov, S.. On thermodynamics of rational maps. II. Non-recurrent maps. J. Lond. Math. Soc. (2) 67(2) (2003), 417–432.CrossRefGoogle Scholar
[15]McCluskey, H. and Manning, A.. Hausdorff dimension for horseshoes. Ergod. Th. & Dynam. Sys. 3(2) (1983), 251–260.CrossRefGoogle Scholar
[16]Palis, J. and Yoccoz, J.-C.. Non-uniformly hyperbolic horseshoes arising from bifurcations of Poincaré heteroclinic cycles. Publ. Math. Inst. Hautes Études Sci. 110 (2009), 1–217.CrossRefGoogle Scholar
[17]Palis, J. and Takens, F.. Fractal dimensions and infinitely many attractors. Hyperbolicity and Sensitive Chaotic Dynamics at Homoclinic Bifurcations (Cambridge Studies in Advanced Mathematics, 35). Cambridge University Press, Cambridge, 1993.Google Scholar
[18]Pesin, Ya. and Senti, S.. Thermodynamical formalism associated with inducing schemes for one-dimensional maps. Mosc. Math. J. 5(3) (2005), 669–678, 743–744.CrossRefGoogle Scholar
[19]Przytycki, F. and Rivera-Letelier, J.. Nice inducing schemes and the thermodynamics of rational maps, 2008.Google Scholar
[20]Rios, I.. Unfolding homoclinic tangencies inside horseshoes: hyperbolicity, fractal dimensions and persistent tangencies. Nonlinearity 14 (2001), 431–462.CrossRefGoogle Scholar