Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-24T00:20:10.820Z Has data issue: false hasContentIssue false
  • English
  • Français

Sylvester matrix rank functions on crossed products

Part of: Rings and algebras arising under various constructions Ergodic theory Homological methods Modules, bimodules and ideals

Published online by Cambridge University Press:  06 June 2019

PERE ARA Open the ORCID record for PERE ARA [Opens in a new window]  and
JOAN CLARAMUNT Open the ORCID record for JOAN CLARAMUNT [Opens in a new window]
PERE ARA
Affiliation:
Departament de Matemàtiques, Universitat Autònoma de Barcelona, 08193Bellaterra (Barcelona), Spain email [email protected], [email protected]
JOAN CLARAMUNT
Affiliation:
Departament de Matemàtiques, Universitat Autònoma de Barcelona, 08193Bellaterra (Barcelona), Spain email [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

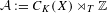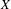In this paper we consider the algebraic crossed product ${\mathcal{A}}:=C_{K}(X)\rtimes _{T}\mathbb{Z}$ induced by a homeomorphism $T$ on the Cantor set $X$, where 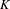$K$ is an arbitrary field with involution and 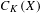$C_{K}(X)$ denotes the 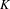$K$-algebra of locally constant 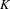$K$-valued functions on 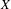$X$. We investigate the possible Sylvester matrix rank functions that one can construct on 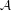${\mathcal{A}}$ by means of full ergodic $T$-invariant probability measures $\unicode[STIX]{x1D707}$ on 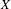$X$. 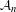To do so, we present a general construction of an approximating sequence of $\ast$-subalgebras ${\mathcal{A}}_{n}$ which are embeddable into a (possibly infinite) product of matrix algebras over 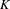$K$. This enables us to obtain a specific embedding of the whole $\ast$-algebra 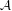${\mathcal{A}}$ into 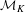${\mathcal{M}}_{K}$, the well-known von Neumann continuous factor over 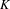$K$, thus obtaining a Sylvester matrix rank function on 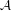${\mathcal{A}}$ by restricting the unique one defined on 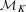${\mathcal{M}}_{K}$. This process gives a way to obtain a Sylvester matrix rank function on 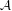${\mathcal{A}}$, unique with respect to a certain compatibility property concerning the measure $\unicode[STIX]{x1D707}$, namely that the rank of a characteristic function of a clopen subset 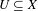$U\subseteq X$ must equal the measure of 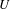$U$.

Keywords

rank functioncrossed productvon Neumann regular ringcompletion

MSC classification

Primary: 16E50: von Neumann regular rings and generalizations
Secondary: 16S35: Twisted and skew group rings, crossed products 37A05: Measure-preserving transformations 16D70: Structure and classification (except as in ), direct sum decomposition, cancellation
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 11 , November 2020 , pp. 2913 - 2946
Check for updates
Copyright
© Cambridge University Press, 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ara, P.. Matrix rings over ∗-regular rings and pseudo-rank functions. Pacific J. Math. 129 (1987), 209–241.CrossRefGoogle Scholar
Ara, P. and Claramunt, J.. Approximating the group algebra of the lamplighter by infinite matrix products, in preparation.Google Scholar
Ara, P. and Claramunt, J.. Uniqueness of the von Neumann continuous factor. Canad. J. Math. 70 (2018), 961–982.CrossRefGoogle Scholar
Ara, P. and Goodearl, K. R.. The realization problem for some wild monoids and the Atiyah problem. Trans. Amer. Math. Soc. 369 (2017), 5665–5710.CrossRefGoogle Scholar
Berberian, S. K.. Baer ∗-rings (Die Grundlehren der mathematischen Wissenschaften, Band 195) . Springer, Berlin, 1972.CrossRefGoogle Scholar
Blackadar, B. and Handelman, D.. Dimension functions and traces on C ∗ -algebras. J. Funct. Anal. 45 (1982), 297–340.CrossRefGoogle Scholar
Claramunt, J.. Sylvester matrix rank functions on crossed products and the Atiyah problem. PhD Thesis, Universitat Autònoma de Barcelona, 2018.Google Scholar
Elek, G.. Lamplighter groups and von Neumann continuous regular rings. Proc. Amer. Math. Soc. 144 (2016), 2871–2883.CrossRefGoogle Scholar
Elek, G.. Infinite dimensional representations of finite dimensional algebras and amenability. Math. Ann. 369 (2017), 397–439.CrossRefGoogle Scholar
Exel, R.. Partial Dynamical Systems, Fell Bundles and Applications (Mathematical Surveys and Monographs, 224) . American Mathematical Society, Providence, RI, 2017.CrossRefGoogle Scholar
Folland, G. B.. Real Analysis: Modern Techniques and Their Applications (Pure and Applied Mathematics (New York)) . Wiley Interscience, New York, 1984.Google Scholar
Giordano, T., Kerr, D., Phillips, N. C. and Toms, A.. Crossed Products of C ∗ -Algebras, Topological Dynamics, and Classification (Advanced Courses in Mathematics, CRM Barcelona) . Birkhäuser, Cham, 2018.CrossRefGoogle Scholar
Giordano, T., Putnam, I. F. and Skau, C. F.. Topological orbit equivalence and C ∗ -crossed products. J. Reine Angew. Math. 469 (1995), 51–111.Google Scholar
Goodearl, K. R.. Von Neumann Regular Rings. Pitman, London, 1979; 2nd edn. Krieger, Malabar, FL, 1991.Google Scholar
Handelman, D.. Completions of rank rings. Canad. Math. Bull. 20 (1977), 199–205.CrossRefGoogle Scholar
Herman, R. H., Putnam, I. F. and Skau, C. F.. Ordered Bratteli diagrams, dimension groups and topological dynamics. Internat. J. Math. 3 (1992), 827–864.CrossRefGoogle Scholar
Jaikin-Zapirain, A.. L 2 -Betti numbers and their analogues in positive characteristic. Groups St Andrews 2017 in Birmingham (London Mathematical Society Lecture Note Series, 455) . Eds. Campbell, C. M., Quick, M. R., Parker, C. W., Robertson, E. F. and Roney-Dougal, C. M.. Cambridge University Press, Cambridge, 2019.Google Scholar
Jaikin-Zapirain, A.. The base change in the Atiyah and the Lück approximation conjectures. Geom. Funct. Anal. 29 (2019), 464–538.CrossRefGoogle Scholar
Jaikin-Zapirain, A. and López-Álvarez, D.. The strong Atiyah Conjecture for one-relator groups. Preprint, 2018, arXiv:1810.12135 [math.GR].Google Scholar
Jaikin-Zapirain, A. and López-Álvarez, D.. On the space of Sylvester matrix rank functions, in preparation.Google Scholar
Kechris, A. S. and Miller, B. D.. Topics in Orbit Equivalence (Lecture Notes in Mathematics, 1852) . Springer, Berlin, 2004.CrossRefGoogle Scholar
Kerr, D. and Li, H.. Ergodic Theory. Independence and Dichotomies (Springer Monographs in Mathematics) . Springer, Cham, 2016.CrossRefGoogle Scholar
Li, H.. Bivariant and extended Sylvester rank functions. Preprint, 2019, arXiv:1901.07158 [math.RA].CrossRefGoogle Scholar
Lück, W.. L 2 -Invariants: Theory and Applications to Geometry and K-Theory (A Series of Modern Surveys in Mathematics, 44) . Springer, Berlin, 2002.CrossRefGoogle Scholar
Malcolmson, P.. Determining homomorphisms to skew fields. J. Algebra 64 (1980), 399–413.CrossRefGoogle Scholar
Murray, F. J. and von Neumann, J.. On rings of operators. IV. Ann. of Math. (2) 44 (1943), 716–808.CrossRefGoogle Scholar
Putnam, I. F.. The C ∗ -algebras associated with minimal homeomorphisms of the Cantor set. Pacific J. Math. 136 (1989), 329–353.CrossRefGoogle Scholar
Putnam, I. F.. On the topological stable rank of certain transformation group C ∗ -algebras. Ergod. Th. & Dynam. Sys. 10 (1990), 197–207.CrossRefGoogle Scholar
Rørdam, M. and Sierakowski, A.. Purely infinite C ∗ -algebras arising from crossed products. Ergod. Th. & Dynam. Sys. 32 (2012), 273–293.CrossRefGoogle Scholar
Rudin, W.. Real and Complex Analysis. McGraw-Hill, New York, 1987.Google Scholar
Schofield, A. H.. Representation of Rings over Skew Fields (London Mathematical Society Lecture Note Series, 92) . Cambridge University Press, Cambridge, 1985.CrossRefGoogle Scholar