Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T00:46:08.715Z Has data issue: false hasContentIssue false
  • English
  • Français

Supramenable groups and partial actions

Published online by Cambridge University Press:  28 January 2016

EDUARDO P. SCARPARO
EDUARDO P. SCARPARO*
Affiliation:
Department of Mathematical Sciences, University of Copenhagen, Universitetsparken 5, DK-2100 Copenhagen, Denmark email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We characterize supramenable groups in terms of the existence of invariant probability measures for partial actions on compact Hausdorff spaces and the existence of tracial states on partial crossed products. These characterizations show that, in general, one cannot decompose a partial crossed product of a 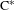$\text{C}^{\ast }$-algebra by a semidirect product of groups into two iterated partial crossed products. However, we give conditions which ensure that such decomposition is possible.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 5 , August 2017 , pp. 1592 - 1606
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ara, P., Exel, R. and Katsura, T.. Dynamical systems of type (m, n) and their C∗ -algebras. Ergod. Th. & Dynam. Sys. 33 (2013), 1291–1325.Google Scholar
Exel, R.. Circle actions on C∗ -algebras, partial automorphisms, and a generalized Pimsner–Voiculescu exact sequence. J. Funct. Anal. 122 (1994), 361–401.Google Scholar
Exel, R.. Partial dynamical systems, Fell bundles and applications, NYJM book series, http://mtm.ufsc.br/∼exel/papers/pdynsysfellbun.pdf, to be published, 2014.Google Scholar
Giordano, T. and Sierakowski, A.. Purely infinite partial crossed products. J. Funct. Anal. 266 (2014), 5733–5764.CrossRefGoogle Scholar
Hjelmborg, J. and Rørdam, M.. On stability of C∗ -algebras. J. Funct. Anal. 155 (1998), 153–170.Google Scholar
Hopenwasser, A.. Partial crossed product presentations for O n and M k (O n ) using amenable groups. Houston J. Math. 33 (2007), 861–876.Google Scholar
Kellerhals, J., Monod, N. and Rørdam, M.. Non-supramenable groups acting on locally compact spaces. Doc. Math. 18 (2013), 1597–1626.Google Scholar
McClanahan, K.. K-theory for partial crossed products by discrete groups. J. Funct. Anal. 130 (1995), 77–117.Google Scholar
Murphy, G. J.. C ∗ -Algebras and Operator Theory. Academic Press, Inc., San Diego, CA, 1990.Google Scholar
Rørdam, M. and Sierakowski, A.. Purely infinite C∗ -algebras arising from crossed products. Ergod. Th. & Dynam. Sys. 32 (2011), 273–293.Google Scholar
Rosenblatt, J. M.. A generalization of Følner’s condition. Math. Scand. 33 (1973), 153–170.CrossRefGoogle Scholar
Rosenblatt, J. M.. Invariant measures and growth conditions. Trans. Amer. Math. Soc. 193 (1974), 33–53.Google Scholar
Wagon, S.. The Banach–Tarski Paradox. Vol. 24. Cambridge University Press, Cambridge, 1993.Google Scholar